De wet van Benford: een inleiding
 In de meeste toepassingen van de statistiek gaat het om getallen die iets betekenen. Ze verwijzen naar de temperaturen in een stad, naar het gemiddeld inkomen per regio of naar het aantal ratten in een bankgebouw. De wet van Benford gaat ook over zulke getallen, maar het vertelt ons, tenminste op het eerste gezicht, niets over de werkelijkheid zelf. Het lijkt alleen maar te gaan over de manier waarop de getallen genoteerd worden. Nadere analyse leert echter dat de werkelijkheid wel degelijk een rol speelt. Maar welke precies is niet helemaal duidelijk.
In de meeste toepassingen van de statistiek gaat het om getallen die iets betekenen. Ze verwijzen naar de temperaturen in een stad, naar het gemiddeld inkomen per regio of naar het aantal ratten in een bankgebouw. De wet van Benford gaat ook over zulke getallen, maar het vertelt ons, tenminste op het eerste gezicht, niets over de werkelijkheid zelf. Het lijkt alleen maar te gaan over de manier waarop de getallen genoteerd worden. Nadere analyse leert echter dat de werkelijkheid wel degelijk een rol speelt. Maar welke precies is niet helemaal duidelijk.Formuleringen van de wet
De meest eenvoudige variant van de wet van Benford stelt dat in een dataset het aantal getallen dat met een 1 begint veel groter is dan het aantal getallen dat met een ander cijfer begint. In een meer omvattende variant wordt voor elk mogelijk begincijfer een kans van voorkomen toegekend waarin die kans afneemt naarmate het begincijfer groter wordt. Deze daling is volgens deze wet logaritmisch. Als p(d) de kans is dat een getal begint met het cijfer d (met d lopend van 1 tot 9) dan wordt deze kans gegeven door:- p(d) = log(d+1) - log(d) = log(1+1/d)

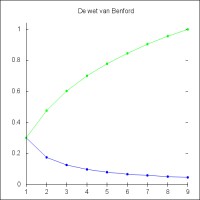 Figuur 1: Kansverdeling volgens Benford
Figuur 1: Kansverdeling volgens Benford- p(1) = 0.301
- p(2) = 0.176
- p(3) = 0.125
- p(4) = 0.097
- p(5) = 0.079
- p(6) = 0.067
- p(7) = 0.058
- p(8) = 0.051
- p(9) = 0.046
De groene lijn in figuur 1 geeft de gesommeerde kansen weer. Voor d = 2, bijvoorbeeld, laat de groene lijn de kans zien dat het getal begint met een 1 of een 2. Deze is uiteraard gelijk aan p(1)+p(2). Het is eenvoudig te bewijzen dat de gesommeerde kans voor alle mogelijke begincijfers inderdaad gelijk is aan 1. Dat bewijs is als volgt:
p(1) + p(2) + ... + p(9) =
(log(2) - log(1)) + (log(3) - log(2)) + ... + (log(10) - log(9)) =
log(10) - log(1) =
1 - 0 =
1
Er bestaan uitgebreidere formuleringen van de wet van Benford die ook de kansen op het voorkomen van cijfers in andere posities weergeven, maar die laten we hier buiten beschouwing.(log(2) - log(1)) + (log(3) - log(2)) + ... + (log(10) - log(9)) =
log(10) - log(1) =
1 - 0 =
1
Wanneer een computer willekeurig getallen genereert dan komen alle begincijfers ongeveer even vaak voor en kan de wet gevoeglijk aan de kant worden geschoven. Maar wanneer de werkelijkheid zelf de data levert - al zijn er veel wiskundige reeksen met dezelfde eigenschap - dan is er een redelijke kans dat de getallen wel de wet van Benford gehoorzamen. Het lijkt een absurde constatering en, als het al waar is, hoogstens een bijzaak waarover de serieuze dataverzamelaar zich niet druk hoeft te maken. Maar het is wel degelijk een patroon en het komt voldoende vaak voor om serieus genomen te worden. Het smeekt om een verklaring.
De praktijk
De ongelijke frequentie van begincijfers komt voldoende vaak voor om praktisch bruikbaar te zijn. Vooral wanneer het om financiële data gaat biedt het een mogelijkheid om gemanipuleerde gegevens van echte gegevens te onderscheiden. Fraude-opsporingsdiensten maken daadwerkelijk gebruik van de wet van Benford om te controleren of er niet ergens iemand met de getallen heeft lopen knoeien. Wanneer mensen getallen verzinnen dan hebben de begincijfers maar zelden de kansen die ze volgens figuur 1 zouden moeten hebben. Er zijn zelfs rechtszaken waarin afwijkingen van de wet als bewijsmateriaal zijn opgevoerd. Als de wet al een bijzaak is, dan is het wel een met consequenties.Een empirische wet
De wet van Benford is een empirische wet. Het is geen stelling die wiskundig is afgeleid van axioma’s of andere stellingen. Het is een patroon dat in veel - maar zeker niet in alle - dataverzamelingen voorkomt. Alles bij elkaar genomen is dat een tamelijk onbevredigende situatie. Iets dat vaak voorkomt zal toch wel een oorzaak hebben? Maar welke? Als die oorzaak bekend is, dan kan misschien ook bepaald worden wanneer de wet wel en wanneer die niet geldt. Naar die oorzaak is men al jaren op zoek en hoewel er inmiddels enige klaarheid in de situatie is gekomen, blijven er nog genoeg vragen over.De twee personen - Simon Newcomb en Frank Benford - die onafhankelijk van elkaar de wet ontdekten, hebben niet alleen het patroon opgemerkt maar ook een mechanisme aangewezen dat het zou kunnen veroorzaken. Beiden voerden de wet van Benford terug tot de volgende tamelijk eigenaardige constatering: wanneer van empirisch gevonden getallen steeds logaritme genomen worden en wanneer die logaritmes uniform verdeeld zijn, dan volgt de wet van Benford. Een uniforme verdeling betekent dat de kans op het voorkomen van een getal in een dataset voor alle getallen even groot is. Een mysterie dat geen van beide ontdekkers tot tevredenheid van iedereen hebben kunnen oplossen, is waarom de logaritmes van zoveel datasets uniform verdeeld zijn. Maar mysteries worden pas interessant als ze begrepen worden. Daarom presenteren we in het volgende de verklaringen van Newcomb en Benford (en anderen) en gaan daarna kort in de op vraag wat er aan schort;
De naam van de wet
Er zijn, als gezegd, twee ontdekkers van de wet van Benford. Van deze was Simon Newcomb veruit de eerste. In 1881 publiceerde hij, zij het in een andere formulering, de wet die hierboven is gegeven. Zijn artikel werd echter nauwelijks opgemerkt en raakte al snel in de vergetelheid. In 1938 herontdekte Frank Benford de wet zonder op de hoogte te zijn van Newcomb's werk. Dat de wet zijn naam kreeg mag dan historisch gezien onjuist zijn, het artikel van Benford is beslist eenvoudiger te volgen en ook nog eens gedetailleerder dan dat van Newcomb. Bovendien heeft hij wel - en Newcomb nauwelijks - de wet getoetst aan de hand van empirisch vergaarde data. Beslist opvallend is dat beide heren de wet op precies dezelfde manier hebben ontdekt, namelijk door op te merken dat sommige boekjes vaker gebruikt werden dan andere.De aanleiding
Ergens rond 1881 kwam Simon Newcomb oog in oog te staan met toentertijd nog gebruikelijk logaritmetafels. De tafels bestonden uit een serie van boekjes waarbij elk boekje getallen bevatte die begonnen met een van de cijfers 1 tot en met 9; voor elk cijfer een apart boekje. Hij zag dat de boekjes voor getallen die begonnen met 1 aanmerkelijk vuiler waren dan de andere boekjes. Komen getallen die met een 1 beginnen dan soms vaker voor? Een andere conclusie was haast niet mogelijk en Newcomb ging op zoek naar een verklaring. Voor die verklaring was nog een andere observatie van belang. De boekjes met anti-logaritmes vertoonden deze afhankelijkheid van het begincijfer niet. De anti-log boekjes beginnend met 1 waren even vuil als de boekjes die begonnen met een 9. Als gezegd, in 1938 constateerde Frank Benford precies hetzelfde. Ook hij ging op zoek naar een verklaring. Om goed te begrijpen waar Newcomb en Benford het precies over hadden, is een korte bespreking van de werking van logaritmetafels nodig.Rekenen met logaritmetafels
Logaritmetafels werden in de tijden van Newcomb en Benford, toen er nog geen computers waren, gebruikt om het vermenigvuldigen van grote getallen te vereenvoudigen. Immers, wanneer z = x * y dan geldt dat log(z) = log(x) + log(y). Als log(z) eenmaal uitgerekend is dan kan men in een ander boekje opzoeken wat de waarde van z is. Deze andere boekjes bevatten wat men toentertijd nog de anti-logaritmes noemde. Op deze manier kon het vermenigvuldigen van getallen vervangen worden door het optellen van de logaritmes. Optellen gaat nu eenmaal veel sneller dan vermenigvuldigen, vooral bij grotere getallen. De drie keren dat een logaritme of anti-logaritme moest worden opgezocht waren weliswaar extra handelingen, maar die wogen niet op tegen de last van het vermenigvuldigen.
Wilde men, bijvoorbeeld, de waarde uitrekenen van 123 * 456, dan werd eerst het logaritme van het getal 123 opgezocht in het boekje met getallen die beginnen met een 1. De waarde ervan is 2,089905 (afgerond op zes decimalen). Hetzelfde werd gedaan voor 456 maar nu uiteraard in het boekje met getallen die beginnen met een 4. De waarde daarvan is 2,658965. De som van beide getallen is 4,748870. Dit is de logaritme van het antwoord en dus is het antwoord gelijk aan 10^[4,748870]. Deze macht van 10 is, als gezegd, het anti-logaritme.
Nu komt er een belangrijke “twist”. In de anti-log tafels wordt niet het getal 4,748870 opgezocht, maar alleen het gedeelte achter de komma, dus 748870. De anti-log van een getal x is immers gelijk aan 10^x en als x geschreven wordt als b + y met b een geheel getal en y een getal tussen 0 en 1, dan hebben we 10^[b+y] = 10^b * 10 ^y. De term b geeft alleen maar aan met welke macht van 10 de anti-log van y vermenigvuldigd moet worden. Met andere woorden, b geeft aan waar de komma moet staan.
Newcomb’s argument
Het raadsel waar Newcomb voor stond was om te verklaren waarom de begincijfers van de getallen waarmee gerekend moest worden - de ruwe data - wel de afhankelijkheid van het begincijfer vertoonden en de logaritmes van die getallen niet. De laatste boekjes waren immers allemaal even vuil. De analyse van Newcomb zullen we hier niet letterlijk volgen. We volgen hier grofweg de analyse van Frank Benford en latere auteurs. Formeel gezien komt het allemaal op hetzelfde neer.
De analyse begint bij een herschrijven van de ruwe data in de wetenschappelijke notatie. Elk getal x kan immers herschreven worden als
- x = a 10^b
waarin a een reëel getal is tussen 1 en 10 (inclusief 1, en exclusief 10) en b een geheel getal is dat negatief, nu of positief kan zijn. Als bijvoorbeeld x = 0,0314 dan kan dit geschreven worden als x = 3,14 * 10^[-2], enzovoort. Wanneer een getal geschreven is in de wetenschappelijke notatie dan heeft de logaritme ervan de volgende verhelderende vorm.
- Als x = a * 10^b dan log(x) = log(a) + b
Het eerste cijfer van x is uiteraard ook het eerste cijfer van a. Het belangrijkste verschil is echter dat we voor x veel verschillende intervallen moeten bekijken (tussen 1 en 1,99..... en tussen 10 en 19,99....., enzovoort) terwijl we in de wetenschappelijke notatie alleen maar naar de a gekeken hoeft te worden. Het getal x begint met een 1 precies dan wanneer a tussen 1 en 2 ligt (exclusief 2 zelf).
De twee observaties van Newcomb (en Benford) kunnen nu met elkaar verbonden worden. De bewering dat het eerste cijfer van x een 1 is hetzelfde als de bewering dat het eerste cijfer van a een 1 is. Dat is op zijn beurt hetzelfde als zeggen dat log(a) tussen log(0) en log(2) ligt, oftewel tussen 0 en 0,301 (afgerond op drie decimalen). Als nu de log getransformeerde getallen uniform verdeeld zijn, dan is de kans dat a ligt tussen 1 en 2 gelijk aan de kans dat a ligt tussen 2 en 3, enzovoort. Terugvertaald naar de data in het ruwe domein betekent dit echter dat de kans dat a begint met een 1 groter is dan de kans dat a begint met een 2. Immers, de eerste kans is gelijk aan log(2) - log(1) = log(2) en de kans op een 2 als eerste begincijfer is gelijk aan log(3) - log(2), enzovoort. Duidelijk is dat deze beweringen precies overeenstemmen met wat de wet van Benford voorschrijft.
De conclusie is duidelijk. Wanneer de logaritmes van de geobserveerde datapunten uniform verdeeld zijn, dan volgen de ruwe data zelf de wet van Benford.
Slotwoord
Benford en Newcomb hebben in abstracto duidelijk gemaakt onder welke condities de wet van Benford kan gelden. Die geldt in elk geval wanneer de logaritmes van de datapunten (= getallen) in een dataset uniform verdeeld zijn. Maar daarmee zijn zeker niet alle problemen uit de wereld geholpen.Het eerste probleem is natuurlijk de vraag waarom de logaritmes van de empirisch vergaarde datapunten uniform verdeeld zijn. Zowel Newcomb en Benford speculeren hierover, maar hun speculaties worden in de regel te vaag gevonden. Ze stellen dat elk geobserveerd getal de resultante is van complexe processen. Denk aan inkomens statistieken. Dat zijn weliswaar eenvoudige getallen, maar de oorzaken (processen) die het getal veroorzaakt hebben zijn zonder enige twijfel immens complex. Newcomb en Benford (en anderen) stellen dat als die processen "multiplicatief" zijn (dus dat er in de formules die allerlei variabelen koppelen aan het inkomen veel vermenigvuldigd moet worden) en wanneer er relatief veel ruis zit in die processen, dat dan verwacht mag worden dat de logs van de datapunten redelijk uniform verdeeld zullen zijn. Dat is geen onredelijk standpunt, maar of het klopt, is een vraag die zowel empirisch als wiskundig verder onderzocht zou moeten worden. Per slot van rekening zijn er ook andere mechanismen denkbaar die tot hetzelfde resultaat leiden.
Een tweede probleem is dat het mechanisme van Newcomb en Benford au fond niet stelt dat de logs van de data uniform verdeeld moeten zijn, maar dat de term log(a) in de wetenschappelijke notatie uniform verdeeld is. Als de de logs van de volledige dataset uniform verdeeld zijn, dan zijn weliswaar de a termen ook uniform verdeeld, maar het omgekeerde hoeft niet te gelden. Er zijn dus "rare" verdelingen denkbaar die wel tot de wet van Benford leiden, maar die niet (volledig) uniform verdeeld zijn
Een derde probleem is dat onduidelijk is of de wet van Benford niet op geen geheel andere manier tot stand zou kunnen komen. Het terugvallen op de logaritmes van geobserveerde data is heel begrijpelijk gezien de context waarin de wet ontdekt is, maar wie zegt ons dat dit de enige manier is waarop zoiets als de wet van Benford (of iets wat er sterk op lijkt) geconstrueerd kan worden?