Kansen en waarschijnlijkheid
Kansen kunnen in vele situaties van pas komen. Hoeveel kans heeft mevrouw X om te genezen van haar kanker? Hoeveel kans heeft meneer Y om de lotto te winnen? Kansen kunnen een handige leidraad zijn bij het nemen van beslissingen (wel of niet behandelen, wel of geen kaartje voor de lotto kopen). In dit artikel wordt ingegaan op de theorie achter kansen.De redenatie achter de statistische gevolgtrekking van kansen berust op het beantwoorden van de volgende vraag: hoe vaak geeft deze methode een correct antwoord wanneer ik het vele malen gebruik?
Wanneer we data verzamelen door willekeurige steekproeven te trekken of willekeurige vergelijkende steekproef experimenten beantwoorden de wetten van de waarschijnlijkheid de volgende vraag: wat gebeurt er wanneer we dit experiment meerdere malen herhalen?
Toevalsverschijnsel
Het gebruik van kans stamt uit de gokwereld. Blaise Pascal en Pierre de Fermat vroege in de 17e eeuw wiskundigen om hulp bij het gokken.Wanneer je een enkele keer met een dobbelsteen gooit kan je het resultaat niet voorspellen, maar na enkele keren gooien zul je wel een patroon ontdekken. Dit is het idee achter kans. Kans beschrijft echter alleen wat er gebeurd op de lange termijn. De meeste mensen verwachten dat kansuitkomsten meer korte termijn regelmaat laten zien dan waar is.
Toeval is in de statistiek geen synoniem voor lukraak, maar is een beschrijving van een soort van orde die verschijnt op de lange termijn. Een verschijnsel wordt toevallig genoemd wanneer de individuele resultaten onzeker zijn maar wanneer er desondanks een gelijkmatige verdeling van resultaten is bij veel herhaling.
De kans van het resultaat van een toevalsfenomeen is de proportie van de keren dat het resultaat zal verschijnen bij veel herhaling. Het idee van kans is niet theoretisch maar gebaseerd op empirie. Kans beschrijft wat er gebeurt bij veel herhaling en we moeten veel proeven observeren om een kans te kunnen vaststellen.
Kans is een mathematisch ideaal, gebaseerd op inbeelden wat er gebeurd in een oneindige serie herhaling. De beste manier om kans te begrijpen is het observeren van toevallig gedrag, niet alleen op de lange termijn maar ook de onvoorspelbare resultaten van korte termijn. Je kunt dit doen met fysieke apparatuur maar software-imitaties geven sneller resultaat.
Opletten!
- Je moet een lange serie van onafhankelijke proeven hebben, zodat de uitkomst van de ene proef de ander niet kan beïnvloeden
- Het idee achter kans is empirisch. Simulaties werken met gegeven kans, de enige manier om ‘real-world’ kans te bereiken is observeren van vele proeven
- Simulaties zijn erg waardevol omdat ze snel kansen kunnen schatten
Modellen van kans
De beschrijving van een toevalsverschijnsel in de wiskunde wordt een kansmodel genoemd.Deze beschrijving bevat:
[OLIST]Uitkomstenruimte (steekproefruimte S, opsomming van mogelijke resultaten)
Gebeurtenis (event, E)
De kans van elk resultaat (probability P)[/OLIST]
De set van mogelijke resultaten van een toevalsverschijnsel wordt uitkomstenruimte genoemd, afgekort tot ‘S’ (van ‘sample space’). Om S te specificeren moeten we er achter komen welke factoren bijdragen aan een individueel resultaat en vervolgens beschrijven welke resultaten mogelijk zijn.
Kans moet niet alleen toegekend worden aan individuele resultaten maar ook aan groepen van resultaten.
Een gebeurtenis is een resultaat of een groep resultaten van een random verschijnsel. Het is een deelverzameling van de uitkomstenruimte. Gebeurtenis wordt afgekort met ‘E’ (van ‘event’)
Voorbeeld: groep jongens of meisjes.
Een kans is een getal dat aan uitkomst of gebeurtenis wordt toegekend en dat aan een aantal regels moet voldoen. Kans wordt afgekort met ‘P’ (van ‘propability’)
Kansregels
Regels waaraan kansen moeten voldoen:
[OLIST]Kans is een getal tussen de 0 en de 1. Elke proportie is een getal tussen de 0 en de 1, dus zo ook elke kans. Een gebeurtenis met als kans 0 komt nooit voor, een gebeurtenis met als kans 1 komt bij elke proef voor.
Wiskundig weergegeven als 0 ≤ P(A) ≤ 1
Alle mogelijke uitkomsten tezamen vormen een kans van 1
Wiskundig weergegeven als P(S) = 1, met S de hele uitkomstenruimte
Wanneer 2 gebeurtenissen geen gemeenschappelijke resultaten hebben is de kans dat een van de twee voor komt de som van hun individuele kansen
Wiskundig weergegeven als P(A of B) = P(A) + P(B)
Dit wordt de ‘algemene rekenregel voor vereniging van gebeurtenissen’ genoemd
De kans dat een gebeurtenis niet voor komt wordt het complement genoemd. Het complement van gebeurtenis A wordt genoteerd als Ac. Volgens de complementregel geldt dat P(Ac) = 1 - P(A) of anders omschreven als P(Ac) + P(A) = 1[/OLIST]
Benford's law
De eerste eenheden van getallen in geldige overzichten volgen vaak een distributie genaamd Benford’s law. Deze wet zegt dat eenheden beginnend met een 1 vaker voorkomen dan eenheden beginnend met een 9, in aflopende volgorde van kans.
In sommige gevallen zijn we geneigd aan te nemen dat individuele resultaten gelijk verdeelde kansen hebben vanwege de balans in het verschijnsel, zoals de fysieke balans tussen de kop en munt van een geldstuk.
Wanneer een random verschijnsel k mogelijke resultaten heeft, allemaal gelijkwaardig, dan heeft ieder individueel resultaat de kans 1 / k.
De kans van een event A is:
De meeste random verschijnselen hebben echter geen gelijkwaardige resultaten, dus de algemene regel voor eenzijdige sample spaces is belangrijker dan de speciale regel voor gelijkwaardige resultaten.
Regel 3 beschrijft de kans dat een van de twee van de events A of B verschijnt in de speciale situatie dat A en B niet tegelijk kunnen verschijnen. De laatste regel beschrijft de kans dat A en B samen verschijnen, tevens in een speciale situatie. Deze regel wordt de vermenigvuldigingsregel genoemd en ziet er als volgt uit:
P (A en B) = P(A) × P(B)
Twee events zijn onafhankelijk wanneer kennis over het verschijnen van de ene de kans dat de andere ook verschijnt niet beïnvloed. De vermenigvuldigingsregel gaat alleen op voor onafhankelijke gebeurtenissen. De vermenigvuldigingsregel gaat op wanneer A en B onafhankelijk zijn maar niet tegengesteld.
De toegevoegde regel voor onsamenhangende events gaat op wanneer A en B onsamenhangend zijn maar niet tegengesteld. Onsamenhangende gebeurtenissen kunnen niet onafhankelijk zijn. Want als A verschijnt, weten we dat B niet kan verschijnen. Wanneer twee events onafhankelijk zijn, dan zijn hun complementen Ac en Bc ook onafhankelijk en is Ac onafhankelijk van B
Random variabelen
Sample spaces hoeven niet persé uit getallen te bestaan. Men kan bijvoorbeeld ook het aantal keer kop tellen.Een random variabele is een variabele wiens waarde een numeriek resultaat geeft op een random verschijnsel.
Er zijn twee manieren om kansmodellen te beschrijven:
- Afzonderlijke random variabelen
- Constante random variabelen
Afzonderlijke random variabelen
Een afzonderlijke random variabele heeft een beperkt aantal mogelijke waarden. Een kans-distributie van X geeft een overzicht van de waarden en hun kansen:
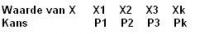
De kans Pi moet voldoen aan twee eisen:
[OLIST]Elke kans Pi is een getal tussen de 0 en de 1
P1 + P2 + … + Pk = 1[/OLIST]
Histogrammen geven de mogelijkheid om de kansen van afzonderlijke random variabelen weer te geven en te vergelijken met andere kansen.
Constante random variabelen
Een constante random variabele is een variabele welke geen afzonderlijke getallen bevat maar een compleet interval aan getallen. De kans-distributie kan beschreven worden met een dichtheidscurve. Ieder individuele waarschijnlijkheid is 0.
