De transformatie van Galileo: afleiding en aannames
 Iemand die aan de kant van de straat staat en kijkt naar voorbijrazende auto's zal ze sneller zien rijden dan iemand in een van die auto’s zit. Met de transformatie van Galileo kan uitgerekend worden hoe snel de bestuurder de auto's ziet bewegen als bekend is hoe snel de toeschouwer aan de kant ze ziet bewegen. En omgekeerd. Het enige dat voor dat uitrekenen bekend moet zijn, is de snelheid van de twee mensen ten opzichte van elkaar. De transformatie wordt niet alleen afgeleid, ook de aannames worden besproken. Die bleken niet allemaal te kloppen en dat vormde de opmaat voor onder andere de speciale relativiteitstheorie.
Iemand die aan de kant van de straat staat en kijkt naar voorbijrazende auto's zal ze sneller zien rijden dan iemand in een van die auto’s zit. Met de transformatie van Galileo kan uitgerekend worden hoe snel de bestuurder de auto's ziet bewegen als bekend is hoe snel de toeschouwer aan de kant ze ziet bewegen. En omgekeerd. Het enige dat voor dat uitrekenen bekend moet zijn, is de snelheid van de twee mensen ten opzichte van elkaar. De transformatie wordt niet alleen afgeleid, ook de aannames worden besproken. Die bleken niet allemaal te kloppen en dat vormde de opmaat voor onder andere de speciale relativiteitstheorie.Inleiding
Twee waarnemers die ten opzichte van elkaar bewegen en beiden kijken naar een bewegend voorwerp zullen de snelheid ervan verschillend waarnemen. Met de transformatie van Galileo kan uitgerekend worden hoe snel beiden het voorwerp zien bewegen. Het enige dat hiervoor nodig is, is de relatieve snelheid van de twee waarnemers. De afleiding van deze transformatie is op zich heel eenvoudig. Tijdens die afleiding worden er - een beetje impliciet - een aantal aannames gemaakt die die teruggrijpen op zeer fundamentele wetten van de klassieke natuurkunde. In de volgende sectie wordt de transformatie afgeleid. In de daarop volgende sectie worden de aannames besproken. Sommige ervan blijken niet te kloppen en vormen in wezen de opmaat voor de speciale relativiteitstheorie.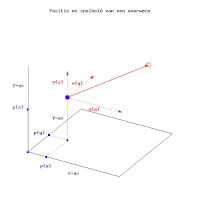 Figuur 1
Figuur 1Afleiding van de transformatie
De positie van een voorwerp kan weergegeven door drie coördinaten omdat de ruimte drie dimensies heeft. Er zijn dus drie assen - X, Y en Z - nodig om de positie (p) van een voorwerp vast te leggen. De coördinaten op deze assen kunnen aangeduid worden met (p(x), p(y), p(z)); p(x) is hier te lezen als de positie van het voorwerp op X-as. De snelheid van een voorwerp heeft zowel een richting als een grootte. De snelheid kan ook als een vector genoteerd worden. Met (v(x), v(y), v(z)) wordt de snelheid langs de drie ruimtelijk assen weergegeven. Een en ander is in figuur 1 weergegeven.De positie wordt bepaald door de drie coördinaten (projecties) op de drie assen te nemen. Dit zijn de blauwe elementen in figuur 1. De snelheid kan ook in drie componenten worden uitgeschreven door te kijken hoe snel het voorwerp zich voortbeweegt langs de drie assen. Dit zijn de rode elementen in figuur 1.
Figuur 1 geeft de situatie weer voor een enkele waarnemer. Om de snelheid van hetzelfde voorwerp te bepalen voor een andere waarnemer die zich met een bepaalde snelheid ten opzicht van de eerste voortbeweegt, kunnen we ons richten op wat er langs de drie assen gebeurt. De snelheid van de tweede waarnemer ten opzichte van de eerste heeft uiteraard ook drie componenten. Met u de relatieve snelheid van de tweede waarnemer kan dit geschreven worden als (u(x), u(y), u(z)). Afstanden worden gemeten in meters en tijd in seconden.
Beschouw als eerste de bewegingen langs de X-as voor de eerste waarnemer. Het voorwerp heeft langs deze as een snelheid v(x). In t seconden heeft het dus een afstand t v(x) afgelegd zodat de nieuwe positie van dit voorwerp na t seconden gelijk is aan p(x) + tv(x). De tweede waarnemer beweegt langs deze as met een snelheid u(x) en legt in t seconden dus t u(x) meter af. Dat betekent dat het voorwerp voor de tweede waarnemer langs de X-as een afstand aflegt van (v(x) - u(x))t.
Precies hetzelfde verhaal kan gehouden worden voor de andere twee assen. De afstand die het voorwerp voor de tweede waarnemer aflegt langs alle assen wordt dus gegeven door de volgende set van vergelijkingen:
- (v(x) - u(x))t
- (v(y) - u(y))t
- (v(z) - u(z))t
De waargenomen snelheden kunnen worden berekend door de afgelegde afstand te delen door de tijd. Voor de tweede waarnemer geldt dan dat deze snelheid, hier w genoemd, gegeven wordt door:
- w(x) = v(x) - u(x)
- w(y) = v(y) - u(y)
- w(z) = v(z) - u(z)
De snelheden van voorwerpen en waarnemers mogen dus bij elkaar opgeteld (of afgetrokken) worden. Zowel de afstand die het voorwerp aflegt volgens de tweede waarnemer als de snelheid van het voorwerp voor hem beweegt zijn hiermee vastgelegd. Het enige dat nog bekend moet zij, is de relatieve snelheid van de twee waarnemers: u. Deze twee sets van vergelijkingen (die in wezen dezelfde zijn) vormen de transformatie van Galileo. De exacte positie van het voorwerp langs de drie ruimtelijke assen kan hieruit eenvoudig bepaald worden wanneer de beginpositie van het voorwerp in beide assenstelsels bekend zijn.
 Figuur 2
Figuur 2Aannames
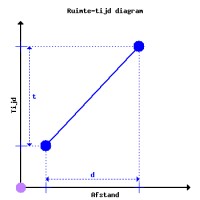
Ruimte-tijd diagrammenDe afleiding is bijzonder eenvoudig, maar toch zijn er een aantal cruciale aannames gemaakt. Een goede manier om die in het vizier te krijgen, is met behulp van een ruimte-tijd diagram. Het belangrijkste kenmerk daarvan is dat de waarnemer zelf in de figuur wordt ingetekend. Minder belangrijk is dat de drie ruimte-assen tot slechts een zijn teruggebracht. Het betekent alleen dat de afstand van het voorwerp tot de waarnemer er toe doet. In een ruimte-tijd diagram (tenminste in de vorm die hier gebruikt wordt) zijn er dus slechts twee assen. De X-as representeert de afstand tussen voorwerp en waarnemer, de Y-as representeert het verloop van de tijd. Figuur 2 geeft dit weer.
Op de oorsprong - de paars gevulde cirkel - staat de waarnemer. De klok is bij aanvang van het experiment op 0 gezet. De afstand van de waarnemer tot zichzelf is altijd gelijk aan 0. Na een tijd verschijnt er een voorwerp in beeld. Dit is de meest links getekende blauwe gevulde cirkel. Deze beweegt en na een poosje het een bepaalde afstand heeft afgelegd. De meest rechtse blauw cirkel is de positie van het voorwerp op een volgend tijdstip. Tijdens de reis heeft het voorwerp een afstand d afgelegd en het had daarvoor een tijd t nodig.
De snelheid van het voorwerp, zeg v kan nu uitgerekend worden door de afgelegde afstand te delen door de benodigde tijd: v=d/t. De snelheid is dus gelijk aan de helling van de lijn.
Eenparige beweging
De transformatie van Galileo werkt alleen voor zogeheten eenparige bewegingen. Dit zijn bewegingen waarop geen krachten inwerken. Volgens de eerste wet van Newton zal het met een constante snelheid en een constante richting voortbewegen. Het is een van de meest belangrijke principes uit de natuurkunde dat - weliswaar in iets gewijzigde vorm - nog steeds overeind staat. De transformatie van Galileo mag alleen gebruikt worden in situaties waarin er geen (of nauwelijks meetbare) krachten op een voorwerp inwerken. Dit is in theorie een vrij strenge aanname maar het in de praktijk valt het wel mee. Wanneer de krachten klein zijn of wanneer de bewegingen bekeken worden over een zeer korte tijdsspanne, dan mag heel vaak aangenomen worden dat ze ten naaste bij eenparig zijn.
De ruimte is in alle richtingen gelijk
In het voorgaande is gezegd dat wat voor bewegingen langs de X-as geldt ook geldt voor bewegingen langs de andere assen. Daaronder ligt echter een zeer fundamentele aanname over de aard van de ruimte. Het stelt namelijk dat de ruimte in alle richtingen dezelfde is. Ook dit is een zeer fundamentele aanname die na jaren experimenteren en theoretiseren nog steeds geldig wordt geacht (al is er ook hier sprake van een aantal modificaties sinds de intrede van de relativiteitstheorie).
Bewegingen zijn altijd relatief
Er wordt bij de afleiding van de transformatie zonder meer aangenomen dat alle bewegingen relatief zijn. Er kan dus alleen sprake zijn van een beweging ten opzichte van andere voorwerpen of waarnemers. Bij de afleidingen is in feite aangenomen dat de snelheid van de eerste waarnemer gelijk aan 0 is. De beweging van het voorwerp met snelheid v is dus een beweging ten opzichte van de eerste waarnemer. Dat is wel degelijk een bijzondere aanname. De grote Newton zelf was het met deze bewering niet eens. Volgens hem bestond er een absolute ruimte ten opzichte waarvan alles beweegt. Newton lijkt hier niet het gelijk aan zijn kant te hebben - al weet je het nooit zeker - maar ook hier geldt dat er onder deze aanname een tamelijk fundamentele mening schuil gaat over wat ruimte (en tijd) nu eigenlijk zijn.
 Figuur 3
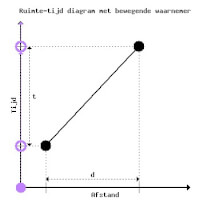
Figuur 3De weergave in de vorige tijd-ruimte diagram (figuur 2) is net iets te eenvoudig. De tijd schrijdt altijd voort en dat betekent dat ook de waarnemer in dit diagram beweegt. Uiteraard blijft de afstand tot hemzelf steeds 0, maar hij (of het) raakt in de tijd wel degelijk steeds meer van zijn oorspronkelijke situatie verwijderd. De paarse cirkel beweegt dus omhoog langs de tijd-as. Zo werkt de tijd nu eenmaal. Een betere weergave van de situatie is gegeven in figuur 3. Deze figuur maakt duidelijker wat het betekent om tijd en afstand te meten.
De waarnemer in figuur 3 noemen we Paars. Paars reist door de tijd en ziet op een gegeven moment een object op een bepaalde afstand van hem. Paars blijft door de tijd reizen en constateert op een volgend moment dat het voorwerp een andere - in dit geval grotere - afstand tot hem heeft.
De hamvraag is nu: hoe meet Paars de afstand van het object? Bij het tekenen van dit diagram werd er vanuit gegaan dat Paars deze afstand op elk moment kan meten. Dat is niet in overeenstemming met de feiten. Om de afstand te meten van een object moeten er signalen naar dat object gestuurd en weer ontvangen worden. Zelfs wanneer men het beeld in het hoofd heeft van een, misschien heel grote, duimstok die tussen een waarnemer en een voorwerp geplaatst kan worden, dan nog moet het uiteinde van de duimstok afgelezen worden. Dat aflezen kan alleen als er een signaal gaat van dat einde naar de waarnemer toe.
Elke meting van afstand kost dus tijd. De enige manier waarop afstand zonder verstrijken van de tijd gemeten kan worden is door aan te nemen dat het signaal een oneindige snelheid heeft. Inmiddels is bekend dat niets sneller gaat dan licht. Oneindige snelheden bestaan niet. Er is dus iets mis met dit gebruik van een ruimte-tijd diagram.
Tenminste, in theorie is er iets mis. In de praktijk valt het reuze mee omdat de signalen die gebruikt kunnen worden (licht dus) weliswaar geen oneindige snelheid hebben maar wel een zeer grote. De tijd die het licht nodig heeft om de afstanden tussen dagdagelijks voorwerpen te meten is zo klein dat het zelfs amper geregistreerd kan worden. Maar in theorie is en blijft het een fout. Het is de speciale relativiteitstheorie die deze fout corrigeert met een aantal spectaculaire gevolgen. Juist omdat voor andere waarnemers dan de eerste de afstand tot het object verschilt zal de tijd die een meting nodig heeft ook voor beide verschillen. Dat simpele feit leidt bijvoorbeeld tot de conclusie dat zowel de gemeten afstand als de gemeten tijd voor beide waarnemers zal verschillen.