Voorbeeld afleiding E = mc²
 E = mc² is de beroemde vergelijking van Einstein die de gelijkwaardigheid van massa en energie uitdrukt. E staat voor energie, m voor massa, en c is de lichtsnelheid. In 1905 kwam Einstein voor het eerst op deze vergelijking uit. Hij baseerde de afleiding uit de Lorentztransformatie van coördinatenstelsels en de aanname dat ether een soort tussenstof waarin alle materie en ruimte is ingebed niet bestaat. In 1946 deed Einstein een andere (eenvoudiger) afleiding die tot hetzelfde resultaat leidt.
E = mc² is de beroemde vergelijking van Einstein die de gelijkwaardigheid van massa en energie uitdrukt. E staat voor energie, m voor massa, en c is de lichtsnelheid. In 1905 kwam Einstein voor het eerst op deze vergelijking uit. Hij baseerde de afleiding uit de Lorentztransformatie van coördinatenstelsels en de aanname dat ether een soort tussenstof waarin alle materie en ruimte is ingebed niet bestaat. In 1946 deed Einstein een andere (eenvoudiger) afleiding die tot hetzelfde resultaat leidt.
Aannames
De afleiding van deze vergelijking uit 1946 berust op een aantal aannames en betrekkingen, die al waren opgesteld door Newton en natuurkundigen in het begin van de 20e eeuw:- p = mv, de impuls van een deeltje
- E = hf = hc/λ, energie van licht is 'omgekeerd proportioneel' met de golflengte λ
- p = E/c =h/λ, de impuls van straling (stralingsdruk)
- Σp voor = Σp na, wet van behoud van impuls
 -fig 1- / Bron: Tronic
-fig 1- / Bron: Tronic- c = lichtsnelheid ≈ 2,998 108 [m/s]
- h = constante van Planck = 6,626 10-34 [Js]
- f = frequentie van het licht [1/s],
- λ = golflengte van het licht [m]
- m = massa [kg], v = snelheid [m/s]
- E = energie van straling (of licht) [J]
De snelheid van het licht is altijd c ≈ 2,998 108 [m/s], ongeacht welke waarnemer het licht bekijkt. Licht kan zowel als golf of als deeltje gezien worden:
- licht gaat dwars door glas (=golf)
- licht wordt weerkaatst door glas (=deeltje)
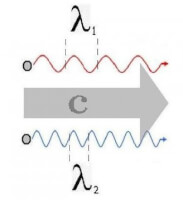
Wanneer we een lichtdeeltje een foton zien als golf, dan is zijn energie gelijk aan E = hc/λ. Wanneer we het als deeltje beschouwen, dan heeft straling een impuls van p = E/c. Zie figuur 1, twee fotonen met verschillende impuls planten zich allebei voort met de lichtsnelheid c; het verschil in energie zit in de verschillende golflengtes (een kortere golflengte λ is een hogere frequentie f en energie E).
E = mc2
 -fig 2- / Bron: Tronic
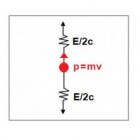
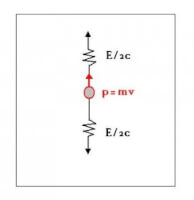
-fig 2- / Bron: TronicStel de massa zendt straling uit met energie E. Vanuit de massa gezien kunnen we dit beschouwen als een helft van deze energie E/2 in de bewegingsrichting v, en de andere helft E/2 in tegenovergestelde richting. De straling heeft een impuls E/2c maar vanuit de massa gezien zijn de impulsen in tegenovergestelde richting even groot, dus vanwege de wet van behoud van impuls zal de snelheid en de impuls van de massa niet veranderen na uitzending van de straling.
Bekijken we dezelfde situatie vanuit de ogen van de doos, dan moeten we concluderen dat de twee golven niet dezelfde (tegengestelde) impuls hebben, en ook dat de energie van de twee golven ongelijk is.
De impuls van de bovenste golf is groter dan die van de onderste, want vanwege de wet van behoud van impuls kunnen we stellen dat de bovenste golf een stukje impuls meekrijgt van de massa (p = mv, naar boven gericht). Het Doppler-effect zorgt ervoor dat de frequentie van de bovenste golf toeneemt (en de golflengte korter wordt).
- de impuls van de bovenste golf neemt toe met (c + v) / c
- de impuls van de onderste golf neemt af met (c - v) / c
De twee golven gaan de doos raken met een netto impuls van p = E / 2c * [(c+v) - (c-v)] / c = Ev / c². De totale impuls voor en na uitzending van de straling moet aan elkaar gelijk zijn.
Totale impuls voor = totale impuls na:
(mv) voor = (mv) na + Ev / c²
De snelheid v is niet beïnvloed, dus de verandering van impuls moet voortgekomen zijn uit een verandering van massa:
- (m,voor - m,na) v = Ev / c²
- Δ m = E / c²
- E = mc ²
Voetnoten
- Gemeten vanuit het oogpunt (coördinatenstelsel) van de massa, is er massa verloren gegaan en omgezet in energie.
- De impuls van de bovenste golf neemt toe met (c + v) / c. De energie van een foton E = hf = hc / λ, als de impuls toeneemt, neemt de energie toe. De lichtsnelheid is constant, dan moet λ veranderen. Relatief gezien komt er (c + v) / c aan bewegingsenergie bij, dus f neemt toe met deze factor. De impuls (p = E / c) verandert ook met (c + v) / c.
- Er is hier een speciaal geval gekozen, namelijk het geval waarbij de 2 impulsen van de straling -vanuit het oogpunt van de massa- elkaar opheffen. In de speciale relativiteit geldt : E = mc² / √(1 - v²/c²). Voor v = 0 geldt dan E = mc².
© 2019 - 2025 Tronic, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Uitvinders: EinsteinEinstein is voor velen gelijk aan de formule E=MC² . Wie heeft daar nog nooit van gehoord? Het is de bekendste wiskundig…
Uitvinders: EinsteinEinstein is voor velen gelijk aan de formule E=MC² . Wie heeft daar nog nooit van gehoord? Het is de bekendste wiskundig…
 Einstein in Nederland, boekbespreking Sybe Izaak RispensEinstein is een icoon geworden en staat symbool voor de geniale mens. Dit beeld is zwaar overdreven. Einstein was een ma…
Einstein in Nederland, boekbespreking Sybe Izaak RispensEinstein is een icoon geworden en staat symbool voor de geniale mens. Dit beeld is zwaar overdreven. Einstein was een ma…
 Vreemdgaan: de afleiding affaireEen van de vele motieven om vreemd te gaan is vreemdgaan te gebruiken als een afleidingsmanoeuvre. Een affaire beginnen…
Vreemdgaan: de afleiding affaireEen van de vele motieven om vreemd te gaan is vreemdgaan te gebruiken als een afleidingsmanoeuvre. Een affaire beginnen…
 Baby Einstein, een educatief programmaBabys moeten tijdens het eerste levensjaar zoveel mogelijk van de buitenwereld zien. Een eenzijdig en beperkt aanbod va…
Baby Einstein, een educatief programmaBabys moeten tijdens het eerste levensjaar zoveel mogelijk van de buitenwereld zien. Een eenzijdig en beperkt aanbod va…
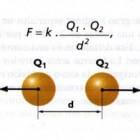 De wet van CoulombTwee elektrische ladingen kunnen een kracht F op elkaar uitoefenen. Deze kracht is vastgelegd in de wet van Coulomb. Naa…
De wet van CoulombTwee elektrische ladingen kunnen een kracht F op elkaar uitoefenen. Deze kracht is vastgelegd in de wet van Coulomb. Naa…
 Rekenen met de lineaire en kubieke uitzettingscoëfficiëntAls je warmte aan een metalen (of anderssoortige) staaf toevoert dan kan deze langer worden of anders gezegd: de lengte…
Rekenen met de lineaire en kubieke uitzettingscoëfficiëntAls je warmte aan een metalen (of anderssoortige) staaf toevoert dan kan deze langer worden of anders gezegd: de lengte…
Gerelateerde artikelen
Bronnen en referenties
- Two exact derivations of the mass/energy relationship, E. Baird
- Out of my later years, A. Einstein, Philosofical library, NY, 1950
- Van spierkracht tot warmtedood, M.J. Sparnaay
- Afbeelding bron 1: Tronic
- Afbeelding bron 2: Tronic
Tronic (33 artikelen)
Gepubliceerd: 11-02-2019
Rubriek: Wetenschap
Subrubriek: Natuurkunde
Bronnen en referenties: 5
Gepubliceerd: 11-02-2019
Rubriek: Wetenschap
Subrubriek: Natuurkunde
Bronnen en referenties: 5
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.