Hoe wordt een T-balk binnen een betonvloer uitgerekend?

Lokaal zwaar belaste vloeren kunnen worden verzwaard met ribben onder de vloer. Ter plaatse van de hoge belastingsconcentratie kan dan van een voordelige inwendige hefboomsarm worden gebruikgemaakt, zodat de stijfheid van die vloer aanzienlijk wordt verbeterd. In dit geval is er geen sprake meer van een vloer, echter een T-balk binnen de constructie van een vloer. Hoeveel breedte aan vloer mag voor deze balk worden meegenomen en hoe wordt de hoofdwapening daarbij berekend?

T-balk in betonvloer uitrekenen

• Verschil tussen een balk en vloer
• Waarom een deel van de vloer meerekenen?
• Wat is de plaats van de wapening?
• Hoe kan de vloer met T-balk concreet worden berekend?

Verschil tussen een balk en vloer

Vloeren zijn standaard relatief dunne constructies, waarbij permanente en variabele belasting als vloerbelasting moeten worden afgedragen. Balken daarentegen vormen de hoofddraagconstructie voor hoge belastingen en zitten meestal langs de rand van vloeren. Indien er echter sprake is van hoog belaste vloeren of plaatselijke concentratie van belasting op de vloer dan is de kans reëel dat de vloer dit niet kan dragen. Om dat op te vangen is er de mogelijkheid om de vloer met plaatselijke ribben uit te voeren. Dit geeft een aanzienlijke verbetering van de stijfheid van de vloer, zodat de belastingen wel kunnen worden afgevoerd.

Waarom een deel van de vloer meerekenen?

Indien binnen een vloer een rib als verstijving wordt toegepast dan is het niet slechts die ribbe waarmee de sterkte wordt behaald. Ook een deel van de vloer neemt de belasting op. Oftewel er ontstaat de omstandigheid, waarbij de vloer en ribbe gaan samenwerken om de belasting te dragen. Hoeveel vloerbreedte daartoe mag worden gerekend is beperkt. Bij een lengte L van de vloer (of twee maal de uitkragingslengte) en een tussenruimte tussen de ribben van L1 en L2, waarbij de ribbe een breedte b heeft dan geldt:

• be = b + b1 + b2;
• b1 = L*0,1 < 0,5*L1;
• b2 = L*0,1 < 0,5*L2.

Wat is de plaats van de wapening?

De bovenwapening kan over de maatgevende constructie over de volledige breedte van ‘be’ worden neergelegd. De onderwapening daarentegen heeft slechts een beperkte breedte en dus kan het zijn dat de korfwapening een redelijke hoeveelheid wapening bevat. Omdat er een goede verhouding ontstaat tussen de mate van toepaste hoeveelheid beton en staalwapening kan er relatief veel belasting worden opgenomen. Er wordt namelijk relatief veel betondrukvlak gerealiseerd in de bovenkant van de brede snede, terwijl de wapening trek in de dunne snede opneemt. Hoe kan één en ander aangaande de vloer- met ribversterkingswapening worden bepaald?

Hoe kan de vloer met T-balk concreet worden berekend?

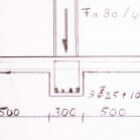
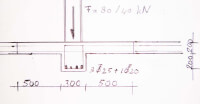
Stel je voor er is sprake van een vloer lang 5 m met een kolombelasting in het midden van 80 kN permanent en 40 kN variabel. De vloer is echter slechts 200 mm dik. Esthetisch gezien is het mogelijk om plaatselijk een versteviging in de vloer te maken, zodat er een inwendige balk (400*300) over de lengte van de vloer ontstaat. Daarnaast wordt de vloer als kantoorruimte gebruikt, waarvoor een variabel gewicht van 2,5 kN/m2 moet worden gerekend. Hoe wordt het afgewapend?

• meewerkende breedte = be = L * 0,1 = 5000 * 0,1 = 500 mm aan weerszijden;
  Bron: Http://geinformeerd.infoteur.nl
• breedte T-balk = 2*500+300 = 1300 mm;
• d = 400-25-8-13 = 354 mm;
• eigen gewicht = 1,0*0,2*24+0,4*0,30*24 +1,5*1,30 = 9,63 kN/m;
• variabel gewicht = 2,5*1,30 = 3,25 kN/m;
• Mrep = 0,125*(9,63+3,25)*5^2+0,25*5*(80+40) = 190,3 kNm;
• Md = maatgevend moment = 0,125*(9,63*1,2+3,25*1,5)*5^2+0,25*5*(1,2*80+1,5*40) = 246,4 kNm;
• Mu / (b*d^2) = 246,4 / (1,30*0,354^2) = 1.512 kN/m2;
• w0 = 0,37 en kx = 0,141 (zie GTB tabellen bij C25 gecombineerd met FeB500);
• xu = 0,141*354 = 50 < 200 mm en dus vormt de betondrukzone netjes binnen de dikte van de vloer;
• As;benodigd = 0,37 * 1,30 * 0,354 * 10^4 = 1.703 mm2;
• As;toegepast = 3 rond 25 met 1 rond 20 = 1.787 mm2.

Check voor scheurvorming

• Tussenafstand staven = (300-25*2-8*2-25*3-20*1)/3 = 46 mm;
• σ;s = 435* 190,3/246,4 * 1.703/1.787 = 320,2 N/mm2;
• ϕmk = 5000/320,2 = 16 mm < 25 mm voldoet niet;
• s;max = 100.000/320,2-130 = 182 mm > 46 mm voldoet wel.

Maximaal opneembaar moment T-balk

• N’b = ¾*15*1.300*xu = 14.625*xu;
• 435*As = 14.625*xu;
• xu = 0,02975*As;
• z = 354-7/18*0,02975*1.787 = 333,3 mm;
• Mu = 1.787*435*333,3 = 259,1 kNm en dus heeft de constructie een UC van 0,95.

Zorg er altijd voor dat hoog belaste constructies zoals een T-balk binnen een vloer concreet worden gecheckt door een ingenieursbureau.

Lees verder

• Hoe reken je een betonvloer uit?
• Ontwerpberekening betonwapening volgens GTB tabellen
• Hoeveel wapening (wapeningspercentage) mag er in beton?
• De versterkte strook betonvloer berekenen en afwapenen
• Voordelen van vierzijdig afgedragen gewapende betonvloeren