Statistiek – Kansberekening

In de statistiek gaat alles om de kans dat X gebeurt. Dit wordt ook wel kansrekening of waarschijnlijkheidsrekening genoemd. Dit kan zinvol zijn voor onderzoek, maar ook praktisch zijn: er kan bijvoorbeeld berekend worden hoe groot de kans is dat er een bepaald aantal patiënten binnengebracht worden in het ziekenhuis en hierop het aantal personeelsleden afstemmen. Hoe bereken je kansen eigenlijk?

Basistermen en notaties

Een kansproces is een proces waarvan de afloop niet bij voorbaat vastligt. Denk bijvoorbeeld aan het gooien van een dobbelsteen: vooraf is onduidelijk hoeveel ogen er gegooid wordt. Elke keer dat het kansproces tot een uitkomst leidt, noemen we dit trekking. Vervolgens moet bepaald worden wat ‘succes’ (of gunstige trekking) betekent: wat wil je onderzoeken? Bij een dobbelsteen kun je succes definiëren als ‘het getal 1 gooien’, maar ook als ‘een oneven getal gooien’. Aan de hand daarvan kan een kans berekend worden.

De kans wordt aangegeven met de letter P (‘probability’). Vervolgens staat tussen haakjes op welke uitkomst de kans betrekking heeft – P(A) betekent dus de kans dat gebeurtenis A optreedt. Dit kan ook gecombineerd worden. P(zwart en plaatje) betekent de kans op een zwarte kaart uit het dek dat ook een plaatje is. Kansen kunnen worden uitgedrukt in een breuk, een decimaalgetal of een percentage. P ligt dus altijd tussen 0 en 1, wat genoteerd wordt als P = 0 of P = 1 (of wat daartussenin ligt).

Soms is de kans op een uitkomst gelijk, zoals bij een dobbelsteen. Hierbij is de kans steeds 1/6, ongeacht welk getal je als succes beschouwt. Bij andere processen is de kans op de ene uitkomst groter dan de kans op een andere uitkomst. Wanneer meerdere uitkomsten succesvol zijn, terwijl elke mogelijke afzonderlijke uitkomst een gelijk kans heeft, dan geldt:

P (succes) = aantal gunstige uikomsten / aantal mogelijk uitkomsten

Een voorbeeld: Stel, je wilt weten hoeveel de kans is dat je 4 gooit met een dobbelsteen. Er zijn zes mogelijkheden en één keer kans op succes (je gooit een 4). De berekening wordt dan: P = 1 / 6 = 1/6 kans op een 4.

Tevens geldt voor een kansberekening dat de kans op succes plus de kans op geen succes samen 1 is. In formule is dat:

P(A) + P(niet A) = 1

Oftewel:
P(A) = 1 – P (niet A)

Het visueel weergeven van kansberekeningen: een kansboom

Een kansboom is een visuele weergave van de kansberekening en helpt overzicht te creëren in alle factoren. Zo kan een dobbelsteen kansboom als volgt worden weergegeven, waarbij elke tak opgeteld weer tot 1 komt: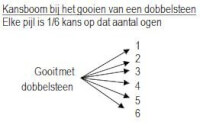

Combinatie van uitkomsten

Veelal zijn niet de afzonderlijke uitkomsten interessant, maar combinaties van uitkomsten. Het kan gaan om meerdere succesvolle uitkomsten zoals P (boer of heer). Ook kan het gaan een ‘en’ situatie, bijvoorbeeld P (vrouw en ouder dan 50 jaar). Verder kun je kijken naar kansen van combinaties van uitkomsten, bijvoorbeeld P (minimaal twee zessen).

Er kan gebruik gemaakt worden van ‘en’, ‘of’ en ‘en/of’ in het aangeven wat een succesvolle trekking is. Zo geeft P (vrouw en/of klaver) een ander beeld dan P (klaver of vrouw). Waarbij bij het eerste de klavervrouw uit het kaartendek succesvol is, is dat in het tweede geval niet meer zo. ‘En’ is dus een inclusievoorwaarde, terwijl ‘of’ een exlusievoorwaarde is.

Optelregel voor het berekenen van ‘en/of’ kansen

Bij ‘en/of’ kansen is het succes afhankelijk van meerdere uitkomsten, bijvoorbeeld P (twee of vier) (hier ‘of’, omdat je niet met één dobbelsteen tegelijk twee en vier kan gooien). Eigenlijk wordt de kans voor twee opgeteld bij de kans op vier – P (twee) plus P (vier). Bij ‘of’ wordt voldoen aan uitsluiten: je kunt immers niet tegelijkertijd twee en vier gooien.

Anders wordt het als je P (boer en/of zwart) wilt berekenen. Hierbij wordt dan de zwarte boeren dubbel geteld. Daarom geldt hier de volgende formule:

P (A en/of B) = P (A) + P (B) – P (A en B)

In het voorbeeld:
P (boer en/of zwart) = P (boer) + P (zwart) – P (boer en zwart)
P (boer en/of zwart) = 4/52 + 26/52 – 2/52 = 28/52

De productregel voor het berekenen van ‘en’ kansen

Bij ‘en’ kansen moet er voldaan worden aan twee of meer voorwaarden. Als het gaat om de uiktkomsten van twee afzonderlijke kansprocessen (kansberekening met ‘teruglegging’ of als voorbeeld opnieuw gooien met de dobbelsteen of de getrokken kaart terugleggen in het dek), dan is de productregel van toepassing.

Stel, je wilt weten hoeveel de kans is dat je twee keer achter elkaar vijf gooit in twee worpen. De kans op één keer 5 is 1/6 en daarna is weer 1/6 kans dat er 5 gegooid wordt (zie kansboom). Vervolgens moeten deze kansen vermenigvuldigd worden.






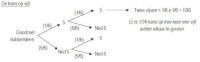
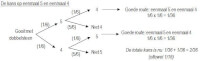
Addertje onder het gras bij de productregel
Stel dat je wilt weten welke kans hoort bij P (eenmaal 5 en eenmaal 4). Hier kun je niet zonder meer de kansen vermenigvuldigen, omdat eer meerdere succesvolle wegen zijn (zie kansboom). Hierbij maakt de volgorde niet uit en worden de verschillende kansen voor succesvolle wegen opgeteld.






Afhankelijke steekproeven
Een afhankelijk steekproef is een steekproef zonder teruglegging. Dit is bijvoorbeeld het geval bij een kaartendek, waarbij je de getrokken kaart niet teruglegt in het dek. De kans dat je een boer trekt wordt dus kleiner als er al een boer uitgetrokken is. De kans op de eerste is namelijk 4/52, terwijl de kans op de tweede boer nog 3/51 is (er gaat één boer af, dus ook één uit het kaartendek). Dit wordt genoteerd als P (boer | boer). De ‘|’ (streepje) staat voor ‘ervan uitgaande dat het ene al is gebeurd’. Dit wordt een voorwaardelijke kans genoemd. Ook hierbij kan de productregel gehanteerd worden, mits op een iets andere manier:

P (A en B) = P (A) x P (B|A)

In het voorbeeld:
P (A en B) = P (boer) x P (tweede kaart is een boer | eerste kaart was boer)
P (A en B) = P (4/52) x P (3/51) = 12/2652

Lees verder

• Statistiek – Permutaties, Variaties en Combinaties
• Statistiek - Binomiaal Toets
• Statistiek - Centrummaten en de normale verdeling