Statistiek – Permutaties, Variaties en Combinaties

Bij een kansberekening wil je weten welke kans er hoort bij een bepaalde gebeurtenis. Verschillende aspecten spelen hierbij een rol. Zo is de volgorde van belang bij het berekenen van het aantal volgordes. Welke manieren hebben we hiervoor?

Kansen

Kansen zijn niets anders dan een percentage die aangeeft hoe groot de kans is dat een gebeurtenis plaats gaat vinden. Dit schrijven we als P van probality. Daarbij gaan we uit van de kans op succes. Met “de kans op succes” wordt bedoeld dat de gebeurtenis plaatsvindt – “succes” is in dit geval dus een neutraal begrip.

Voorbeeld

Je wilt berekenen hoe groot de kans is dat je een harten boer trekt. Dit schrijf je als volgt:

P (harten boer) = aantal gunstige uitkomsten / aantal mogelijke uitkomsten

Faculteit

Een faculteit wordt genoteerd als “a!”. De “a” is in dit geval een getal en “!” wordt uitgesproken als faculteit. Dit betekent dat a! betekent dat je a*(a-1)*(a-1)*…*1. In een voorbeeld: 4!=4*3*2*1. Daarnaast geldt dat 1! en 0! altijd 1 is. Ook geldt dat een faculteit vóór andere berekeningen komt (voor machten, wortels, vermenigvuldigen, delen, optellen en aftrekken).

Permutaties

Een permutatie gaat over de manieren waarop iets gerangschikt kan worden. Als je het hebt over muntjes A, B, C en D en je hebt plaats I, II, III en IV. Als ik alleen munt A wil neerleggen, heb ik hiervoor 4 opties. Als ik A en B neer wil leggen, dan heb ik 4*3=12 opties. Een permutatie (P) is het aantal mogelijkheden als je alle muntjes gebruikt. Dit wordt als volgt geschreven:

Voorbeeld

Als je 6 boeken wil rangschikken en je vraagt je af op hoeveel manieren dat kan, dan is dit 6! manieren. Dit betekent dat je 6*5*4*3*2*1=720 verschillende manieren hebt om de boeken neer te zetten.

Merk op dat de volgorde van het plaatsen hier niets uitmaakt!

Variaties

Stel dat je nu nog alleen munt A en B hebt, maar nog steeds plaats I, II, III en IV. Zoals gezegd, heb je hiervoor 4*3=12 mogelijkheden. Echter, dit kan je niet schrijven als 4!, want dan klopt de berekening niet. Daarom spreken we dan van variatie. De formule hiervoor ziet er als volgt uit: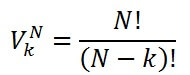


In deze formule is V de variatie, N het aantal mogelijkheden en k de objecten die je wilt plaatsen.

Voorbeeld

Stel dat je 3 boeken hebt, maar je hebt 6 plaatsen in de boekenkast. De som wordt dan:


Hierbij is de volgorde wel van belang: je legt eerst munt/boek A weg, dan pas B enzovoort.

Combinaties

Stel nu dat het niet uitmaakt in welke volgorde de successen zijn, als de paren maar goed zijn. Je kunt dus zowel AB als BA trekken. Dan ziet de formule er als volgt uit: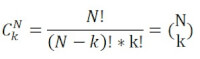

Dit laatste spreek je uit als “N boven k”.

Voorbeeld

Stel je hebt 4 mensen waaruit je 2 mensen wilt trekken, maar waarbij de volgorde niet uitmaakt. Je kunt dan AB of BA trekken. Dit schrijf je als volgt:


Merk hierbij op dat de volgorde van trekken er dus niet toe doet!

Lees verder

• Statistiek – Kansberekening
• Statistiek - Binomiaal Toets
• Statistiek - Meetniveaus en statistiek
• Statistiek - Centrummaten en de normale verdeling