De vierkleurenstelling
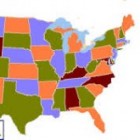De vierkleurenstelling houdt in, dat je een landkaart met oneindig veel landen kunt inkleuren met maar vier kleuren, zonder dat daarbij twee buurlanden dezelfde kleur krijgen. Er zijn wel enkele randvoorwaarden: de landen moeten een aaneengesloten oppervlak hebben en de kaart moet vlak of bolvormig zijn. Al in de renaissance kleurde men kaarten in met maar vier kleuren, maar pas in de negentiende eeuw vroeg men zich af of deze stelling ook wiskundig te bewijzen is.Het probleem
Degene die zich als eerste in 1852 afvroeg of de vierkleurenstelling wiskundig te bewijzen viel, was Francis Guthrie. Als student aan het University College in Londen zocht hij zelf naar het bewijs, maar het lukte hem niet dat te vinden. Hij liet het zijn broer voorleggen aan diens docent, de bekende wiskundige Augustus De Morgan. Die kwam er niet uit en schakelde weer andere wiskundigen in, maar zoals wel vaker bleek de vraag eenvoudiger dan het antwoord. Een eerste aanzet tot bewijs werd in 1878 gepubliceerd door Arthur Cayley. Hij bewees dat het volstond om te kijken naar landkaarten waarbij steeds drie landen in een punt bij elkaar komen.
Bron: Inductiveload, Wikimedia Commons (CC BY-SA-3.0)Eerste oplossing
Een jaar na Cayley kwam Alfred Bray Kempe, een van zijn oud-studenten, met de eerste poging tot bewijs van de vierkleurenstelling. Op 17 juli 1879 publiceerde hij een artikel in het tijdschrift Nature, naar aanleiding waarvan hij de onderscheiding Fellow Of The Royal Society ontving. Echter, in 1890 toonde de Engelse wiskundige Percy John Heawood aan, dat het bewijs van Kempe fouten bevatte. Vervolgens besteedde diezelfde Heawood zestig jaar van zijn leven om zelf het bewijs te vinden, tevergeefs. Wel wist hij te bewijzen dat vijf kleuren volstaan om een landkaart in te kleuren.De oplossing
Pas in 1976 werd door Kenneth Appel en Wolfgang Haken weer een algemeen bewijs voor de vierkleurenstelling gepubliceerd. Voor die tijd waren er wel wat ‘deelbewijzen’ geleverd. Zo bewees Franklin in 1922 dat de stelling klopt voor alle kaarten met 25 landen of minder. Appel en Haken gebruikten voor hun bewijs de uitgangspunten van Kempe. Daarnaast brachten zij het probleem terug tot een beperkt aantal gevallen (toch nog zo’n 1500), waardoor de controleberekeningen door een computer konden worden verricht. Die deed daar zo’n 1200 uur over.Wetenschappers als Neil Robertson, Daniel Sanders, Paul Seymour en Robin Thomas in de jaren negentig en George Gonthier in 2004 wisten de probleemstelling nog verder te vereenvoudigen, waardoor uiteindelijk ook de controleberekeningen van de computer door een computer gecontroleerd konden worden.
