De geschiedenis van pi
 Het magische getal pi. Een geheimzinnig, maar ook interessant getal. We hebben het allemaal op school bij de wiskundeles gehad. Vanaf het begin van de wiskunde heeft het getal tal van wiskundewetenschappers geïntrigeerd. Veel takken van de wiskunde maken gebruik van het getal pi: onder andere meetkunde, getallentheorie en kansberekening.
Het magische getal pi. Een geheimzinnig, maar ook interessant getal. We hebben het allemaal op school bij de wiskundeles gehad. Vanaf het begin van de wiskunde heeft het getal tal van wiskundewetenschappers geïntrigeerd. Veel takken van de wiskunde maken gebruik van het getal pi: onder andere meetkunde, getallentheorie en kansberekening.
Pi
Pi = π = 3,14159265359... De definitie van pi is de verhouding tussen de omtrek en de diameter van een cirkel, oftewel:pi = omtrek van de cirkel / diameter van de cirkel
Het getal pi is een irrationeel getal, misschien wel het bekendste irrationele getal. Dit betekent dat pi niet te berekenen is als deling van twee getallen: er is geen breuk die pi kan beschrijven. Daarnaast is de cijferreeks achter de komma bij het getal pi oneindig. Het bevat ook geen repeterende patronen, het is telkens anders.
Babyloniërs
De geschiedenis van pi begint al in 1936 v.Chr. bij de Babyloniërs. In Susa, een stad in het huidige Iran, zijn een aantal kleitabletten gevonden. Op een van deze kleitabletten staan berekeningen waaruit blijkt dat de rekenaar een constante waarde heeft gebruikt voor het berekenen van de oppervlakte van een cirkel. Deze berekende waarde was 3 + 1/8 oftewel 3,125Egyptenaren
De Egyptenaren schreven in 1650 v.Chr. al in de Rhind papyrus over de oppervlakte van een cirkel. In de Rhind papyrus was dit een van de 87 wiskundige problemen. De Egyptisch priester Ahmes berekende pi door aan te nemen dat de oppervlakte van een cirkel met diameter 9 gelijk is aan de oppervlakte van een vierkant met zijdes van 8. Hij berekende pi dus als volgt: pi × (9/2)² = 8². De berekende waarde van pi bij de Egyptenaren was dus: 3,16046Bijbel
Ook in de bijbel (rond 950 v.Chr.) wordt pi uitgerekend. In het boeken 2 Kronieken 4:2 en 1 Koningen 7:23 wordt geschreven dat Salomo ‘een bekken van gegoten brons, vijf el hoog, met een middellijn van tien el en een omtrek van dertig el’ liet maken. Als we ervan uit mogen gaan dat het bekken de vorm van een cirkel had, kan geconcludeerd worden dat in de tijd van de bijbel de waarde van pi gelijk was aan 3.Oude Grieken
Archimedes (287-212 v.Chr.) was de eerste persoon die doorhad dat pi niet exact berekend kon worden. Hij schrijft hierover in een van zijn boeken: ‘Het opmeten van de cirkel’. In dit boek beschrijft hij de methode die hij gebruikte om pi te benaderen. Hij toont in het boek aan dat pi ligt tussen de 223/71 en 22/7.Hij benaderde de omtrek van een cirkel door binnen en buiten de cirkel een regelmatige rechthoek te tekenen. Van deze rechthoeken kon hij de omtrek berekenen. Hierdoor wist hij dat de omtrek van de cirkel die tussen de rechthoeken lag, tussen de omtrek van deze twee rechthoeken lag: een benadering van pi. Door het aantal hoeken van de rechthoeken steeds te verdubbelen, kon hij steeds exacter pi berekenen. De benadering van Archimedes van pi door het insluiten van de cirkel door twee rechthoeken met 96 hoeken kwam uit op: 3,140845 < pi < 3,142857.
China
In China hield de wiskundige Zu Chongzhi zich rond 480 n.Chr zich bezig met pi. Zu Chongzhi is zeker 1000 jaar recordhouder gebleven voordat de waarde van pi weer werd verbeterd. Hij benaderde de omtrek van een cirkel door de cirkel te vergelijken met een rechthoek met 24,576 (= 213 × 3) hoeken. Hij berekende op deze manier dat pi moest liggen tussen 3.1415926 en 3.1415927Arabische wereld
Al-Kashi, een beroemde Arabische wiskundige, heeft rond 1430 de benadering van de Chinees Zu Chonqzhi verbeterd. Ook hij gebruikte de methode van Archimedes door de omtrek van de cirkel te benaderen door hier veelhoeken voor te gebruiken. Hij gebruikte voor berekening een veelhoek met 805306368 zijden. Hierdoor berekende Al-Kashi pi als 3,14159265358979.Europa
Na jaren van stilte op het wiskundige vlak, begon men in Europa zich in de zestiende eeuw bezig te houden met het berekenen van het getal pi. In 1593 berekende de Fransman François Viète met behulp van de methode van Archimedes de waarde van pi. Hij gebruikte hiervoor een veelhoek met 393216 zijden. Hij berekende pi als 3,1415926536. Merk op dat de waarde van pi in de Arabische wereld al nauwkeuriger was berekend, met meer decimalen achter de komma.Rond dezelfde tijd berekende de Duits/Nederlandse wiskundige Ludolph van Keulen (1540-1610) het getal pi tot 35 decimalen achter de komma.
De naam ‘pi’
In 1706 kreeg de constante eindelijk de naam pi. Tot die tijd heette de constante ‘de constante van Archimedes’.Meer decimalen achter de komma
Het getal pi was aardig benaderd. Het enige wat nog verbeterd kon worden was het aantal decimalen achter de komma. William Shank (1812 – 1882), een Britse amateur wiskundige, berekende pi tot 707 cijfers achter de komma. Deze benadering van pi werd als standaard verheven totdat in 1944 bleek dat er een fout zat in de berekening: vanaf het 527e getal klopt het niet meer. Door de uitvinding van de computer was het mogelijk om pi tot ver achter de komma te berekenen. Het wereldrecord anno 2015 staat op 10 triljoen cijfers.© 2015 - 2025 4chevaux, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Pi, getallen tot in het oneindigeHet getal Pi, oneindig gebruikt in de wiskunde, met oneindig veel decimalen achter de komma. Wat is ‘het geheim’ achter…
Pi, getallen tot in het oneindigeHet getal Pi, oneindig gebruikt in de wiskunde, met oneindig veel decimalen achter de komma. Wat is ‘het geheim’ achter…
 Omtrek berekenen van een wiskundig figuurHet komt regelmatig voor dat je moet weten wat de omtrek van iets is. Het is daarom handig om te weten hoe je de omtrek…
Omtrek berekenen van een wiskundig figuurHet komt regelmatig voor dat je moet weten wat de omtrek van iets is. Het is daarom handig om te weten hoe je de omtrek…
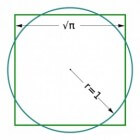 Kwadratuur van de CirkelHet was een onopgelost geometrisch probleem voor de oude Grieken en dat zou het nog heel lang blijven: hoe construeer je…
Kwadratuur van de CirkelHet was een onopgelost geometrisch probleem voor de oude Grieken en dat zou het nog heel lang blijven: hoe construeer je…
 Wiskunde - radialenWanneer je aan de slag gaat met cirkels wordt al snel met het begrip 'radialen' gewerkt. De radiaal is een maat om aan t…
Wiskunde - radialenWanneer je aan de slag gaat met cirkels wordt al snel met het begrip 'radialen' gewerkt. De radiaal is een maat om aan t…
 Geschiedenis van de Romeinse cijfersDe Romeinse cijfers, we kennen ze allemaal. Ze staan vaak afgebeeld op klokken, als geboortedatum, op standbeelden of bi…
Geschiedenis van de Romeinse cijfersDe Romeinse cijfers, we kennen ze allemaal. Ze staan vaak afgebeeld op klokken, als geboortedatum, op standbeelden of bi…
 Het algoritme van EuclidesMet het algoritme van Euclides kan op een eenvoudige en zeer efficiënte manier de grootste gemene deler van twee getalle…
Het algoritme van EuclidesMet het algoritme van Euclides kan op een eenvoudige en zeer efficiënte manier de grootste gemene deler van twee getalle…
Gerelateerde artikelen
Bronnen en referenties
- Inleidingsfoto: Geralt, Pixabay
- http://info.gsf.nl/cdb/ddb/Onderbouw/Wiskunde/toetsen/H1lj2/pi/pigeschiedenis.htm
- http://www.isgeschiedenis.nl/nieuws/oorsprong-van-het-getal-pi/
- http://www.wiskunde.net/pi
- http://en.wikipedia.org/wiki/Zu_Chongzhi
4chevaux (102 artikelen)
Laatste update: 01-06-2015
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 5
Laatste update: 01-06-2015
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 5
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.