Kwadratuur van de Cirkel
Het was een onopgelost geometrisch probleem voor de oude Grieken en dat zou het nog heel lang blijven: hoe construeer je een vierkant dat hetzelfde oppervlak heeft als een gegeven cirkel? Dat wiskundigen geen oplossing konden vinden voor dit probleem bleek in de negentiende eeuw niet zo vreemd; het is namelijk helemaal niet mogelijk om dat vierkant te construeren. Dit heeft te maken met een getal dat van groot belang is voor de eigenschappen van een cirkel: het getal pi.Het probleem van de kwadratuur van de cirkel heeft tijdens zijn gehele geschiedenis veel aantrekkingskracht gehad. Het probleem is simpel te stellen: gegeven een cirkel, construeer het vierkant dat hetzelfde oppervlak heeft als de cirkel met alleen liniaal en passer. De oplossing van het probleem bleek echter veel ingewikkelder.
Het probleem bestond al ver voor onze jaartelling bij o.a. de Egyptenaren. Het was echter bij de oude Griekse wiskundigen dat het probleem zijn definitieve vorm kreeg en de eerste serieuze pogingen werden gedaan om een oplossing te vinden.
Het getal π
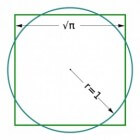
Het getal π (3.1415....) komt in veel gebieden van de wiskunde terug, maar de klassieke definitie is dat π de verhouding is tussen de omtrek van een cirkel en zijn diameter. De Griekse wiskundige Archimedes bewees dat dit getal tevens van belang is voor het oppervlak van een cirkel. Daarvoor geldt namelijk A = π r^2, waar A het oppervlak is en r de straal van de cirkel. Voor een vierkant is het oppervlak natuurlijk het kwadraat van de lengte van de zijden, dus willen we voor een cirkel met straal r het bijbehorende vierkant construeren, dan moet dat een vierkant worden met zijden van lengte r √π. Dat laatste blijkt problematisch.Al snel kregen wiskundigen door dat π niet zomaar een getal is. Archimedes wist de waarde van π te benaderen: hij bewees dat de waarde moest liggen tussen 223/71 en 22/7 door een cirkel te benaderen met regelmatige veelhoeken. Eeuwenlang maakten wiskundigen betere benaderingen, maar een exacte waarde bleef buiten hun greep. Hoe verder ze gingen in hun berekeningen, hoe meer decimalen π kreeg en er leek geen einde aan te komen en daarmee bleef ook een constructie voor de kwadratuur van de cirkel uit.
De onmogelijkheid van de kwadratuur
Grote wiskundigen van Archimedes tot Descartes bogen zich over het probleem, zonder een oplossing te kunnen vinden. Het kwadrateren van de cirkel werd zelfs een uitdrukking die betekende dat men het onmogelijke aan het proberen was. Het zou uiteindelijk 2000 jaar duren voordat er uitsluitsel over het probleem was.In de jaren 60 van de achttiende eeuw wist Johann Heinrich Lambert te bewijzen dat π een speciaal soort getal was, namelijk een zogenaamd irrationeel getal. Irrationele getallen zijn getallen die niet kunnen worden geschreven als breuk. Dit heeft tot gevolg dat deze getallen oneindig veel decimalen hebben en dat die decimalen ook geen patroon vertonen. Veel wiskundigen kregen hierdoor al het idee dat de kwadratuur van de cirkel inderdaad een onoplosbaar probleem is en verloren hun interesse ervoor. Het bewees echter in principe nog niet dat het construeren van het juiste vierkant onmogelijk was.
Het duurde nog eens honderd jaar, maar in 1882 kwam dan uiteindelijk het definitieve antwoord. De Duitse wiskundige Ferdinand Lindemann wist te bewijzen dat π niet alleen irrationeel is, maar zelfs transcendent. Transcendente getallen vormen een subset van de irrationele getallen, volgens een nog beperktere definitie. Een van de eigenschappen van transcendente getallen is dat ze niet kunnen worden voorgesteld met een constructie met passer en liniaal. Het feit dat π transcendent is, betekent dus dat het vierkant dat men zocht helemaal niet geconstrueerd kan worden!
