Wiskunde - Rekenen met machten
Rekenen met machten kan heel makkelijk zijn, maar ook heel gecompliceerd. Machten komen in elke tak van de wetenschap voor: in de natuurkunde bij de berekening van de centrifugaalkracht, in de scheikunde bij het rekenen aan een concentratiebreuk en in de wiskunde bij polynome functies. Rekenen met machten is zodoende een vaardigheid die goed moet beheerst moet worden. Er bestaan rekenregels voor berekeningen aan machten die dergelijke berekeningen makkelijker maken.De macht
Een macht is, simpel gezegd, een cijfer dat rechtsboven een getal hangt. De macht vertelt hoe vaak het cijfer maal zichzelf moet. In het geval van 35 betekent dit dus dat het cijfer 3, het grondgetal, vijf maal met zichzelf moet worden vermenigvuldigd. De notatie 35 is zodoende een afgekorte notatie van 3 * 3 * 3 * 3 * 3, waarvan de uitkomst 243 is. De macht geeft dus eigenlijk aan in welke hoeveelheid het grondgetal maal zichzelf moet. Toch bestaan er ook machten die onder de 1 liggen. Zo bestaat er ook 21/2. Een breuk als macht moet altijd als volgt worden opgevat, tevens is het handig een kommagetal om te zetten naar een breuk:- Bij een breuk als macht is de teller altijd de macht die wordt geheven over het grondgetal
- Bij een breuk als macht is de noemer altijd de n-de wortel die moet worden getrokken van grondgetalteller
Zodoende is 21/2 gelijk aan √2, en 34/3 is gelijk aan 3√(34).
Rekenregels bij machten
Duidelijk is dat er een regel bestaat voor het heffen van machten die kleiner zijn dan 1. Er bestaan nog meer rekenregels voor machten.De kern van deze rekenregels is dat dit enkel en alleen kan met grondgetallen die hetzelfde zijn.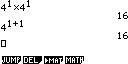
Figuur 1: machten van 4Beschouw het getal 4. Het getal 4 is, met macht geschreven, 41. Vermenigvuldig 4 met 4 en de uitkomst is 16. 16 is een getal dat kan worden geschreven in machten van 4: 42. De vermenigvuldiging 4 * 4 = 16 kan dus ook geschreven worden als 41 * 4 1 = 42. Een ander voorbeeld: 5 * 25 is gelijk aan 125. 25 en 125 zijn machten van 5 (25 kan geschreven worden als 5 * 5, 52, en 125 als 5 * 5 * 5, 53), dus die vergelijking kan worden geschreven als 51 * 52 = 53. Voor het optellen van machten in een vergelijking geldt dus:
ap * aq = ap+q.
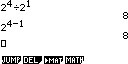Figuur 2: machten van 2Het optellen van machten is laten zien, waarbij dezelfde grondgetallen met verschillende machten maal elkaar resulteren in het grondgetal tot de macht van de som van de machten. De machten kunnen ook van elkaar afgetrokken worden door een deling. Beschouw 16 / 2. De uitkomst is 8. 16 kan uitgedrukt worden in 2 * 2 * 2 * 2, oftewel 24. 8 kan uitgedrukt worden in 2 * 2 * 2, oftewel 23. In een dergelijke deling krijgt men dan 24 / 21 = 24-1 = 23. Ook hier blijft het grondgetal hetzelfde; het is niet mogelijk om andere grondgetallen te gebruiken bij een dergelijke berekening. Voor het aftrekken van machten geldt zodoende:
ap / aq = ap-q.
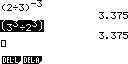Figuur 3: negatieve machten en inversieEen negatieve macht kan ook voorkomen. Een negatieve macht houdt in dat de breuk wordt geïnverteerd. Beschouw het voorbeeld 2-2. De negatieve exponent zegt niets meer dan dat het grondgetal verandert naar 1 / grondgetal. In dit geval betekent het dus dat de 2 verandert naar 1/2. Maar daar stopt het niet. Het negatieve is nu doorgevoerd, maar de tweede macht is nog niet doorgewerkt. De tweede macht wordt geheven over de hele term, oftewel, (1/2)2. Dit resulteert in 1/4. In figuur 3 is een deelteken gebruikt in plaats van een breuk; bij gebruik van een breuk zou hetzelfde antwoord voortkomen. Gebruik bij delingen breuken altijd haken wanneer er machten worden geheven.
Bij een breuk gebeurt precies hetzelfde. Het handigste om te doen is om eerst het negatieve gedeelte van de macht te behandelen, die houdt enkel de inverse van de term in. (2/3)-3 wordt zodoende (3/2)3. Vervolgens wordt de macht over de gehele term geheven, wat geeft (33) / (23) = 27 / 8.
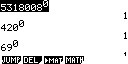Figuur 4: de nulde macht, uitkomst is altijd 1Bij een grondgetal tot de macht 0 is het antwoord altijd 1. Het maakt niet uit hoe groot het grondgetal a is: of dit 8, 92, 178, 10603 of ∞ is, als over het grondgetal een macht 0 wordt geheven is de uitkomst altijd 1.
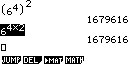Figuur 5: vermenigvuldigen van machtenSoms wordt over een bestaand grondgetal met macht nog een macht geheven. In dat geval is de nieuwe macht het product van allebei de machten. Als voorbeeld wordt 64 beschouwd. 64 is gelijk aan 6 * 6 * 6 * 6 = 1296. Als hierover nog een tweede macht wordt geheven, zoals 2, dan is de vergelijking feitelijk (64)2. Hieruit komt 64 * 2 = 68. Hierbij geldt zodoende
(ap)q = ap * q
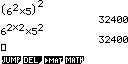
Indien er meerdere grondgetallen zijn en daarover een macht wordt geheven, verandert er feitelijk niks. Indien grondgetal a en b aanwezig zijn, waarbij grondgetal a wordt geheven tot de macht 6, dan is het resulterende product a6b. Wordt over dit product nog een macht geheven, zoals 5, dan is de uitkomst (a6b)5 = a6 * 5b5 = a30b5
