Vergelijkingen oplossen (3): exponentiële vergelijkingen
 In dit deel zullen we verschillende soorten exponentiële vergelijkingen bespreken en oplossen. Exponentiële vergelijkingen hebben veel praktische toepassingen buiten de wiskunde. Voorbeelden hiervan zijn de berekening van samengestelde rente, radioactief verval en bevolkingsgroei.
In dit deel zullen we verschillende soorten exponentiële vergelijkingen bespreken en oplossen. Exponentiële vergelijkingen hebben veel praktische toepassingen buiten de wiskunde. Voorbeelden hiervan zijn de berekening van samengestelde rente, radioactief verval en bevolkingsgroei.
Definitie
Een exponentiële vergelijking is een vergelijking met ten minste een term van de vorm af(x). Hierbij is a een constante en f(x) is een functie van x. f(x) kan een willekeurige functie zijn, bijvoorbeeld f(x) = 2x + 4 of gewoon f(x) = x. Met a = 3 en f(x) = 2x + 4 krijgen we de exponentiële term 32x+4.Voorbeelden van exponentiële vergelijkingen zijn:
1) 1,05x = 2
2) 22x+4 = 16384
3) 42x-5 = 4x+3
4) 8x = 4x+2
5) 34x+1 = 6x+2
2) 22x+4 = 16384
3) 42x-5 = 4x+3
4) 8x = 4x+2
5) 34x+1 = 6x+2
Exponentiële vergelijkingen oplossen
We bespreken drie soorten exponentiële vergelijkingen die we zullen oplossen:af(x) = b
af(x) = ag(x)
af(x) = bg(x)
af(x) = ag(x)
af(x) = bg(x)
Vergelijkingen in de vorm af(x) = b
In de eerste soort vergelijkingen staat links een exponentiële term af(x) en rechts een constante b. Een voorbeeld van een vergelijking in deze vorm is voorbeeld 1:1,05x = 2
Om deze vergelijking op te lossen, moeten we aan beide kanten de logaritme nemen:
log (1,05x) = log 2
Nu kunnen we een belangrijke truc toepassen die gebaseerd is op de volgende regel:
log (ap) = p * log a
We mogen de exponent dus gewoon buiten de haken halen! Als we dit toepassen op de term log (1,05x), krijgen we:
x * log 1,05 = log 2
Nu kunnen we x eenvoudig uitrekenen:
x = log 2 / log 1,05 = 0,301 / 0,021 = 14,2
Een controle geeft:
1,0514,2 = 2
De oplossing klopt dus!
Ook het tweede voorbeeld werkt op dezelfde manier:
22x+4 = 16384
We nemen eerst aan beide kanten de logaritmen:
log (22x+4) = log 16384
Ook hier mogen we de exponent buiten de haken halen:
(2x + 4) * log 2 = log 16384
Nu is x eenvoudig uit te rekenen:
2x + 4 = log 16384 / log 2 = 4,214 / 0,301 = 14
2x = 10
x = 5
2x = 10
x = 5
Tot slot de controle:
22*5+4 = 214 = 16384
De oplossing klopt!
Vergelijkingen in de vorm af(x) = ag(x)
In de tweede soort vergelijkingen staat zowel links als rechts een exponentiële term. Hier hebben beide termen echter hetzelfde grondtal a. Dit maakt het oplossen van deze soort vergelijkingen een stuk makkelijker. Het blijkt namelijk dat we dan geen logaritmen nodig hebben! Voorbeeld 3 is al in deze vorm, maar we kunnen ook voorbeeld 4 in deze vorm herschrijven.We laten eerst zien waarom voorbeeld 3 eenvoudig is op te lossen:
42x-5 = 4x+3
In een exponentiële vergelijking waarbij beide kanten hetzelfde grondtal hebben, moeten ook de exponenten gelijk zijn. Anders gaat de vergelijking niet meer op! We kunnen hier dus eenvoudig zeggen:
2x - 5 = x + 3
Nu hebben we een lineaire vergelijking die eenvoudig is op te lossen:
x - 5 = 3
x = 8
x = 8
Een controle geeft:
42*8-5 = 411
48+3 = 411
48+3 = 411
De oplossing klopt dus.
Ook als de grondtallen niet gelijk zijn, is het soms mogelijk om de vergelijking te herschrijven tot een vergelijking waar de grondtallen wel gelijk zijn. Een voorbeeld hiervan is voorbeeld 4:
8x = 4x+2
Beide grondtallen (4 en 8) zijn machten van 2. Immers, 22 = 4 en 23 = 8. Als beide grondtallen machten van hetzelfde getal zijn, kunnen we de termen herschrijven. In dit geval gaan we beide termen herschrijven in machten van 2.
Voor het herschrijven maken we gebruik van de volgende regel:
(ap)q = ap*q
Met behulp van deze regel kunnen we 8x herschrijven:
8x = (23)x = 23x
Ook kunnen we 4x+2 op deze manier herschrijven:
4x+2 = (22)x+2 = 22x+4
Als we dit invullen in de oorspronkelijke vergelijking, krijgen we:
23x = 22x+4
De grondtallen zijn gelijk, dus zijn de exponenten dat ook:
3x = 2x + 4
x = 4
x = 4
Tot slot de controle:
84 = 4096
44+2 = 46 = 4096
44+2 = 46 = 4096
De oplossing klopt dus.
Vergelijkingen in de vorm af(x) = bg(x)
Deze soort vergelijkingen hebben ook aan beide kanten een exponentiële term. Hier verschillen de grondtallen echter, wat de oplosmethode een stuk lastiger maakt. Voorbeeld 5 is een voorbeeld van deze vorm:34x+1 = 6x+2
De oplosmethode is in grote lijnen hetzelfde als bij de eerste vorm. We nemen eerst aan beide kanten de logaritmen:
log (34x+1) = log (6x+2)
Ook nu halen we de exponenten buiten de haken:
(4x + 1) * log 3 = (x + 2) * log 6
We moeten nu de haken wegwerken:
4x * log 3 + log 3 = x * log 6 + 2 * log 6
Er ontstaat nu een lineaire vergelijking. We halen dus alle termen met x naar de ene kant en de constanten naar de andere kant:
4x * log 3 - x * log 6 + log 3 = 2 * log 6
4x * log 3 - x * log 6 = 2 * log 6 - log 3
4x * log 3 - x * log 6 = 2 * log 6 - log 3
We ontbinden het linkerdeel in factoren, om zo x apart te krijgen:
x * (4 * log 3 - log 6) = 2 * log 6 - log 3
Nu moeten we alleen nog delen door (4 * log 3 - log 6):
x = (2 * log 6 - log 3) / (4 * log 3 - log 6)
x = (2 * 0,778 - 0,477) / (4 * 0,477 – 0,778)
x = (1,556 – 0,477) / (1,908 – 0,778)
x = 1,079 / 1,130 = 0,955
x = (2 * 0,778 - 0,477) / (4 * 0,477 – 0,778)
x = (1,556 – 0,477) / (1,908 – 0,778)
x = 1,079 / 1,130 = 0,955
Tot slot de controle:
34*0,955+1 = 34,819 = 199,2
60,955+2 = 62,955 = 199,2
60,955+2 = 62,955 = 199,2
De oplossing klopt!
Hopelijk weet je met deze technieken genoeg om exponentiële vergelijkingen op te lossen!
© 2008 - 2025 Arjen, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Vergelijkingen oplossen(1): lineaire vergelijkingenIedereen die op de middelbare school wiskunde heeft, krijgt te maken met wiskundige vergelijkingen. Misschien ben je hie…
Vergelijkingen oplossen(1): lineaire vergelijkingenIedereen die op de middelbare school wiskunde heeft, krijgt te maken met wiskundige vergelijkingen. Misschien ben je hie…
 Vergelijkingen oplossen(2): kwadratische vergelijkingenIn het tweede deel van deze serie gaan we kwadratische vergelijkingen oplossen. De kwadratische vergelijking is een stuk…
Vergelijkingen oplossen(2): kwadratische vergelijkingenIn het tweede deel van deze serie gaan we kwadratische vergelijkingen oplossen. De kwadratische vergelijking is een stuk…
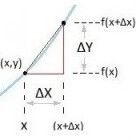 Wiskunde de afgeleide en differentiërenDe afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y).…
Wiskunde de afgeleide en differentiërenDe afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y).…
Gerelateerde artikelen
Vergelijkingen oplossen met algebraIn de moderne wiskunde is oplossen met algebra steeds belangrijker aan het worden. In iedere lesmethode is hier iets ove…
Stelsels van lineaire vergelijkingen oplossenEen stelsel van lineaire vergelijkingen bestaat uit meerdere vergelijkingen en heeft meerdere onbekenden. We bespreken h…
De geschiedenis van de getallen en het tellenTellen begon lang voordat er symbolen zoals 1, 2 en 3 voor de afzonderlijke getallen waren. In feite kan men tellen zond…
Bronnen en referenties
- http://users.telenet.be/chris.cambre/chris.cambre/exponentiele_vgln.htm http://nl.wikipedia.org/wiki/Exponenti%C3%ABle_groei
Reactie
Peronista (infoteur), 16-12-2008 #1
Jemig, studeer je wiskunde ofzo? Het ziet er allemaal wel heel ingewikkeld uit!:-)
Reactie infoteur, 17-12-2008
Klopt, het is ook best ingewikkeld hoor! :-) Vooral het laatste stuk is niet eenvoudig. Er wordt wel verondersteld dat je lineaire vergelijkingen goed kunt oplossen, want anders is het niet te doen. Maar als ik ergens niet duidelijk ben in mijn artikel, stuur maar een berichtje of laat een reactie achter!
Arjen (6 artikelen)
Gepubliceerd: 08-12-2008
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 1
Gepubliceerd: 08-12-2008
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 1
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.