Het bewijzen van de stelling van Pythagoras

In dit artikel wordt uitgelegd hoe de stelling van Pythagoras op twee manieren bewezen kan worden. Het is geschreven voor geïnteresseerden die hun inzicht in deze beroemde stelling willen vergroten. Verder is er voor het begrijpen van dit bewijs vrijwel geen wiskundige voorkennis nodig, behalve het bekend zijn met de stelling zelf. Er zijn tegenwoordig ruim driehonderd verschillende bewijzen gevonden voor de stelling van Pythagoras. Veel hiervan vereisen veel wiskundige voorkennis en zullen in dit artikel dus niet aan bod komen.

Bewijs #1

Om te beginnen zal hieronder een algebraïsch bewijs worden geleverd, waarbij gebruik wordt gemaakt van het onderstaande figuur: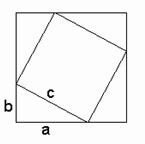


Hier is te zien dat de oppervlakte van het gedraaide vierkant gelijk moet zijn aan c². De lengte van elke zijde van het grote vierkant is a + b, waardoor de oppervlakte ervan gelijk moet zijn aan (a + b)². Dit kan ook geschreven worden als a² + 2ab + b². Verder kan er met twee van de vier driehoeken een rechthoek gevormd worden waarvan één zijde gelijk is aan a, en de ander aan b. De oppervlakte van zo'n rechthoek is dus ab. Omdat er in totaal vier driehoeken zijn, kunnen er twee rechthoeken worden gevormd, met een totale oppervlakte van 2ab.

Met deze drie definities kan nu een bewijs worden opgesteld. In het figuur is te zien dat de oppervlakte van het gedraaide vierkant (c²) gelijk moet zijn aan de oppervlakte van het grote vierkant (a² + 2ab + b²), min de oppervlakte van de vier driehoeken (2ab). Wanneer dit wordt uitgeschreven ontstaat:

• (a + b)² - 2ab = c²
• a² + 2ab + b² - 2ab = c²
• a² + b² = c²

Bewijs #2

Het volgende bewijs is in de twaalfde eeuw gevonden door de hindustaanse wiskundige Bhaskara, en lijkt enigzins op het vorige bewijs. Met vier gelijke driehoeken (met zijden a, b, en c) kan het vierkant dat hier linksonder te zien is worden gevormd: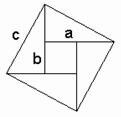


Net als bij bewijs #1 bevat het grote vierkant vier driehoeken, met een totale oppervlakte van 2ab. Het kleine vierkant in het midden heeft zijden met lengte (a - b), en dus een oppervlakte van (a - b)². En het grote vierkant heeft weer een oppervlakte van c².

In het figuur is te zien dat de totale oppervlakte van de vier driehoeken (2ab) samen met het kleine vierkant ((a - b)²), gelijk moet zijn aan de oppervlakte van het grote vierkant (c²). Er ontstaat dan opnieuw een vergelijking, die erg veel op de vorige lijkt:

• (a - b)² + 2ab = c²
• a² - 2ab + b² + 2ab = c²
• a² + b² = c²

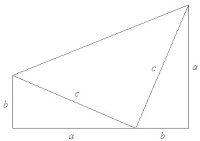
Bewijs #3

Dit bewijs is in 1876 door President J.A. Garfield ontdekt. Het lijkt opnieuw op de vorige twee bewijzen, maar er wordt hier geen gebruik gemaakt van vierkanten. Dit bewijs maakt gebruik van een trapezium. Het oppervlak van een trapezium wordt gegeven door: h(a + b) ÷ 2, waarin a en b de lengten van respectievelijk de kleine en grote basis zijn, en h de hoogte van het trapezium is. Als het trapezium 90° wordt gedraaid, is te zien dat de hoogte ervan gelijk is aan a + b, en de twee basen gelijk zijn aan a en b. Het oppervlak van het trapezium wordt dan:

(a + b)(a + b) ÷ 2 = (a + b)² ÷ 2.

De som van de oppervlakten van de losse driehoeken in het trapezium is gelijk aan:

ab ÷ 2 + ab ÷ 2 + c² ÷ 2 = ab + c² ÷ 2.

Als deze twee definities worden vergeleken, ontstaat de stelling van Pyhtagoras:

• (a + b)² ÷ 2 = ab + c² ÷ 2
• (a + b)² = 2ab + c²
• a² + 2ab + b² = 2ab + c²
• a² + b² = c²