Priemgetallen begrijpen
Priemgetallen zijn waarschijnlijk de meest bekende getallen binnen de wiskunde, en dan met name getaltheorie. Maar wat zijn priemgetallen? En wat maakt ze bijzonder? In dit artikel is onder andere uitgelegd hoe je kunt aantonen dat er oneindig veel priemgetallen bestaan, en dat elk getal deelbaar is door priemgetallen.Priemgetallen
- Wat zijn priemgetallen?
- Elk getal bestaat uit priemgetallen
- Bewijzen dat elk getal bestaat uit priemgetallen
- Bewijzen dat er oneindig veel priemgetallen bestaan
- De grootste bekende priemgetallen
Wat zijn priemgetallen?
Priemgetallen zijn natuurlijke getallen (natuurlijke getallen zijn 1, 2, 3, enzovoorts) die slechts twee positieve delers hebben. Meestal wordt gezegd dat priemgetallen alleen deelbaar zijn door zichzelf, en een. Dit is geen goede definitie omdat het getal 1 ook aan deze eis voldoet, terwijl het geen priemgetal is. Als een getal priem genoemd wordt, betekend dit simpelweg dat het een priemgetal is (bijvoorbeeld: "3 is priem, 4 is niet priem").Elk getal bestaat uit priemgetallen
Hieronder is een tabel te zien met daarin de getallen 2 t/m 28. Hier valt op dat elk natuurlijk getal dat niet priem is, het product is van getallen die wel priem zijn. Om deze reden worden priemgetallen ook wel de elementen van de natuurlijke getallen genoemd. Net zoals moleculen zijn opgebouwd uit atomen, zijn de getallen die niet priem zijn opgebouwd uit priemgetallen.| Getal | Opbouw | Getal | Opbouw | Getal | Opbouw |
|---|---|---|---|---|---|
| 2 | Priem | 11 | Priem | 20 | = 2×2×5 |
| 3 | Priem | 12 | = 2×2×3 | 21 | = 3×7 |
| 4 | = 2×2 | 13 | Priem | 22 | = 2×11 |
| 5 | Priem | 14 | = 2×7 | 23 | Priem |
| 6 | = 2×3 | 15 | = 3×5 | 24 | = 2×2×2×3 |
| 7 | Priem | 16 | = 2×2×2×2 | 25 | = 5×5 |
| 8 | = 2×2×2 | 17 | Priem | 26 | = 2×13 |
| 9 | = 3×3 | 18 | = 2×3×3 | 27 | = 3×3×3 |
| 10 | = 2×5 | 19 | Priem | 28 | = 2×2×7 |
Bewijzen dat elk getal bestaat uit priemgetallen
"Elk getal dat niet priem is, is het product van priemgetallen". Zo luidt de Hoofdstelling van de rekenkunde. Maar hoe weten we eigenlijk dat dat klopt? Het is namelijk niet te controleren aangezien er oneindig veel getallen zijn. Er is echter een manier om simpel te beredeneren dat dit waar moet zijn:Het bewijs
Stel dat er getallen bestaan die niet het product zijn van priemgetallen. Er bestaat dan ook een kleinste getal dat niet het product is van priemgetallen (en zelf geen priemgetal is), dit getal noemen we X. X moet deelbaar zijn door niet-priemgetallen (anders is het zelf een priemgetal). Maar we weten dat alle getallen die kleiner zijn dan X, wel het product zijn van priemgetallen (X was namelijk het kleinste getal dat dat niet was), of zelf priemgetallen zijn. In beide gevallen is X deelbaar door priemgetallen, en dus het product van priemgetallen.
Bewijzen dat er oneindig veel priemgetallen bestaan
Dit is natuurlijk ook niet te controleren, aangezien er oneindig veel getallen zijn. Dat er oneindig veel priemgetallen bestaan is zeker, en wordt de de stelling van Euclides genoemd. De stelling is te bewijzen door aan te tonen dat het onmogelijk is dat er niet oneindig veel priemgetallen bestaan:Het bewijs
Stel dat er slechts een x aantal priemgetallen bestaat. We noemen deze priemgetallen P1, P2, P3.... Tot en met Px. Als je al deze priemgetallen met elkaar vermenigvuldigt, ontstaat er een getal dat deelbaar is door al deze priemgetallen. Wanneer je bij dit getal 1 optelt, krijg je een getal dat door geen van de eerder genoemde priemgetallen deelbaar is.
Dit betekend dat dit getal zelf priem is, òf dat het deelbaar is door een ander priemgetal dat nog niet bekend was (want eerder was al bewezen dat elk getal priem is, of het product is van priemgetallen). In beide gevallen bestaan er meer priemgetallen dan degene die we hadden genummerd. Er bestaan dus oneindig veel priemgetallen.
De grootste bekende priemgetallen
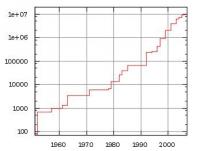
Er zijn oneindig veel priemgetallen, waardoor je nooit het grootste priemgetal kunt vinden. Er worden tegenwoordig steeds grotere priemgetallen gevonden. Op dit moment is het grootste bekende priemgetal gelijk aan: 243,112,609 − 1. Als dit getal volledig wordt uitgeschreven, is het 12,978,189 cijfers lang. Het getal is 23 Augustus 2008 ontdekt met een project genaamd GIMPS (Great Internet Mersenne Prime Search).Maar aangezien computers steeds sneller worden, kunnen er steeds grotere priemgetallen worden gevonden. Hieronder is een tijdlijn te zien waarin het aantal cijfers van het grootste bekende priemgetal is verwerkt.