Hoeken berekenen met de tangens functie

Op de middelbare school krijgt bijna elke leerling te maken met het berekenen van hoeken. De ene leerling krijgt dit op een eenvoudige manier, door zelf een schatting te maken van de hoek met behulp van een geodriehoek, en de ander leert om met de tangens functie hoeken te berekenen. In dit artikel staat stap voor stap uitgelegd hoe je hoeken berekend met de tangens functie op je rekenmachine

Hoeken berekenen

Bijna elke leerling van een middelbare school krijgt les over hoeken berekenen. Hoe hoger het niveau van de opleiding, hoe moeilijker, maar ook exacter de functies om hoeken te berekenen worden. In dit artikel staat uitgelegd hoe je een hoek berekend aan de hand van de tangens functie, een wiskundige term op de rekenmachine waarmee hoeken berekend kunnen worden als de lengte van twee zijden van de driehoek bekend zijn.

Geodriehoek

Het gemakkelijkste is om bij het berekenen van hoeken een geodriehoek te gebruiken. Zo kun je hoeken aflezen, en als het nodig is zelf narekenen. Een geodriekhoek is in veel zaken waar schoolspullen of kantoorspullen verkocht worden te koop en kost ongeveer 50 eurocent. Je hebt flexibele geodriehoeken, die minder snel breken, en plastic driehoeken die vaak het voordeligste zijn.

Hoeken berekenen met de tangens

De tangens is een term waarmee je de hoeken kunt berekenen als de overstaande en de aanliggende zijde van de hoek die berekend moet worden bekend zijn. In de tekening hieronder staan de overstaande zijde, de aanliggende zijde, en de schuine zijde van hoek A weergegeven.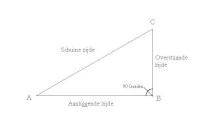

Let wel op: Als je hoek C moet berekenen zijn de aanliggende en de overstaande zijde anders dan bij hoek A. We hebben het in dit voorbeeld dus alleen over de berekening van hoek A

Een ezelsbruggetje om te helpen onthouden welke zijde je bij de tangens moet gebruiken is TOA. Dit betekent dat je voor de tangens de overstaande en de aanliggende zijde moet weten.

Tangens = overstaande zijde / aanliggende zijde.

Stel de overstaande zijde is 5 centimeter lang, en de aanliggende zijde 8 centimeter. Dan deel je dus 5 (de overstaande zijde) door 8 (de aanliggende zijde). Het antwoord van de som 5/8 is 0,625. Dit is nog niet het gehele antwoord, er moet nog verder worden gerekend.

Graden

De uitkomst van de hoek die je berekend hebt is 0,625 maar hoeken worden vaak in graden weergegeven. Nu moet je dus 0,625 naar graden berekenen. Hiervoor zit een knop op je rekenmachine: Tan. Echter moet je niet de Tan knop hebben maar SHIFT (of 2ND) + TAN intoetsen, er staat dan waarschijnlijk TAN-1 op je rekenmachine. Toets TAN-1(0,625) en druk op enter. Nu zie je 32,00 staan in je venster. Dit betekent dat de hoek dus 32 graden is. Leg voor de zekerheid je geodriekhoek even op de hoek en kijk of het antwoord klopt, je geodriehoek zal wel sneller iets afwijken van de werkelijkheid omdat het moeilijk is om een hoek exact af te lezen.

Procenten

Langs de weg zie je vaak de helling van de weg in procenten weergegeven. Dit kan ook, doe het antwoord 0,625 x 100% = 62,5% de helling is dus 62,5 %

Lees verder

• De lengte van een zijde van een driehoek berekenen
• Hoeken berekenen met de cosinus
• Hoeken berekenen met de sinus