De lengte van een zijde van een driehoek berekenen

Op de middelbare school krijg je vaak les over de cosinus, de sinus en de tangens. Aan de hand van twee lengtes van een driehoek kun je het aantal graden van een hoek berekenen. In dit artikel gaan we aan de hand van een graden van een hoek en een lengte de lengte van een andere zijde van een driehoek berekenen.

Hoeken berekenen

Hoeken berekenen is een basisonderwerp van wiskunde. Iedereen krijgt er mee te maken, maar de een op een eenvoudigere manier dan de ander. De een mag met zijn geodriekhoek een hoek berekenen terwijl de ander met formules hoeken moet berekenen. Naast de hoeken berekenen kun je ook nog te maken krijgen met het berekenen van de lengte van een zijde van een driehoek. Hierover wordt in dit artikel meer uitgelegd.

De basis van het berekenen van hoeken en lengtes van zijde is het werken met de cosinus, sinus en tangens, drie functies op je rekenmachine. Vaak leer je als eerste aan de hand van twee lengtes van zijdes het aantal graden van een hoek te berekenen. Dit doe je met de onderstaande formules.

• Sinus = overstaande zijde / schuine zijde
• Cosinus = aanliggende zijde / schuine zijde
• Tangens = overstaande zijde / aanliggende zijde

Om een hoek te kunnen berekenen moeten er dus twee zijdes bekend zijn. Aan de hand van de bekende zijdes bepaal je of je sinus, cosinus of tangens gebruikt. Het antwoord wat uit deze som komt is nog niet het aantal graden van de hoek. Als je sinus hebt gebruik doe je sin -1 en de uitkomst van je som, dan heb je het aantal grades. Als je tangens of cosinus hebt gebruikt vul je deze in gevolgd door -1 (vaak shift sinus, cosinus of tangens)

De lengte van een zijde berekenen

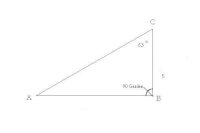
Je wilt nu de lengte van een zijde van een driehoek berekenen. Hiervoor heb je één lengte van een zijde nodig, en één graden van een hoek. Aan de hand van deze twee gegevens kun je een andere lengte van een zijde berekenen.

Op de afbeelding zie je dat er een graden van een hoek bekend is, de graden van hoek C, namelijk 63 graden. Ook weet je een lengte van een zijde namelijk 5, de lengte van C naar B.

Je kunt nu kiezen om de schuine zijde te berekenen, de zijde van A naar C, of de overstaande zijde van hoek C, de zijde van A naar B. In dit voorbeeld kiezen we ervoor om de schuine zijde te berekenen, zijde AC.

Je weet de aanliggende zijde van hoek C, die heeft namelijk een lengte van 5. Je weet ook het aantal graden van hoek C namelijk 63. Je wilt de schuine zijde weten. Je gaat nu zoeken naar een formule waarin de zijde zit die je al weet: De aanliggende zijde, en waar de zijde in zit die je wilt weten, de schuine zijde.

Je kiest dus om de cosinus te gebruiken, daar zit immers de aanliggende zijde en de schuine zijde in. Je weet ook de cosinus, dus de formule die je gaat invullen is als volgt:
Cosinus 63 = 5 (aanliggende zijde) / ? (schuine zijde)

Eerst tik je op je rekenmachine cos 63 in, het getal dat hieruit komt is 0,454. Nu krijg je dus:
0,454 = 5 (aanliggende zijde) / ? (schuine zijde)

Om achter het vraagteken te komen deel je 5 door 0,454.

Vraagteken onder de streep = delen (/)
Vraagteken boven de streep = keer (*)

Dit antwoord, 5 / 0,454, is 11.01. De lengte van de schuine zijde is dus 11.01.

Lees verder

• Hoeken berekenen met de cosinus
• Hoeken berekenen met de sinus
• Hoeken berekenen met de tangens functie