Complexe getallen
 In het dagelijks leven rekenen we met getallen uit de reële verzameling R. Complexe getallen, of getalparen, zijn een uitbreiding hierop. De uitbreiding op een reëel getal is het imaginaire gedeelte van een complex getal: j = √-1. We nemen aan dat de wortel uit een negatief getal bestaat, en dat een complex getal z = x + jy. De getallen (x) en (y) zijn onderdeel van R, maar (z) is onderdeel van C, de verzameling complexe getallen.
In het dagelijks leven rekenen we met getallen uit de reële verzameling R. Complexe getallen, of getalparen, zijn een uitbreiding hierop. De uitbreiding op een reëel getal is het imaginaire gedeelte van een complex getal: j = √-1. We nemen aan dat de wortel uit een negatief getal bestaat, en dat een complex getal z = x + jy. De getallen (x) en (y) zijn onderdeel van R, maar (z) is onderdeel van C, de verzameling complexe getallen.Complex getal
Normaliter zijn we gewend om met getallen te uit de verzameling N of R rekenen, dat wil zeggen:- we gebruiken getallen uit de reeks natuurlijke getallen (N) 0, 1, 2, 3..,, 35, 36, 37, .....,
- of uit de verzameling reële getallen (R) = (N), met als uitbreiding gebroken-, of kommagetallen.
Zo is het getal 5,67391 een getal uit de verzameling R. Complexe getallen zijn een uitbreiding op de reële getallenverzameling. Een complex getal bestaat uit een reëel en een imaginair gedeelte, om het imaginaire gedeelte aan te duiden, nemen we aan:
- het getal j = √-1
- j ² = -1
De notatie voor een complex getal is:
- z = x + j y
Alle getallen of getalparen (x,y) die een complex getal vormen zijn onderdeel van de verzameling complexe getallen C. Deze uitbreiding op R (of R²) levert nieuwe rekenmethodes op.
Complexe getallen zijn te beschouwen als elementen van een twee-dimensionale ruimte; hiermee kunnen we allerlei problemen zichtbaar maken (en oplossen) in het complexe vlak, rekenen met vectoren (pijlen), en oplossingen vinden voor vergelijkingen met periodieke functies. De twee dimensies zijn:
- variabele x = reële gedeelte (z)
- variabele y = imaginaire gedeelte (z)
Het complexe vlak
algemene notatie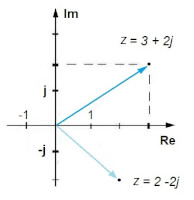 -fig 1- / Bron: Tronic
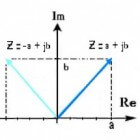
-fig 1- / Bron: TronicStel een complex getal z = a + jb, dan zal dit getal een punt in het complexe vlak voorstellen met coördinaten (a,b) - zie figuur 1:
het punt (3,2) of z = 3 + 2j is aangeduid met de stippellijnen. Wanneer het reële gedeelte van een complex getal gelijk is aan nul, schrijft men z = 0 + jb = jb (=0,1).
Het getal z = j kan men dus noteren als:
- z = j
- (0,1)
Rekenregels voor complexe getallen zijn:
optellen
vermenigvuldigen
reciproke
delen
- (a + jb) + (c + jd) = (a+b + j(c+d))
vermenigvuldigen
- (a + jb) * (c + jd) = (ac-bd + j(ad+bc))
reciproke
- 1/(a + jb) = (a - jb)/(a² + b²)
delen
- (a + jb)/(c + jd) = [(ac + bd) + j(bc - ad)]/(c² + d²)
 -fig 2- / Bron: Tronic
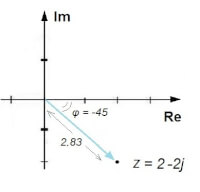
-fig 2- / Bron: TronicVoor de lengte en de richting van een vector geldt:
- lengte = | z | = √ [ (im)² + (re)² ]
- richting = argument = arctangens [im/re]
voorbeeld van de vector die wijst naar P(2,-2):
lengte = √ [ (im)² + (re)² ] = √ [ 2² + (-2)² ] = √ 8 ≈ 2.83
argument = arctg [im/re] = arctg [-2/2] = arctg [-1] = - 45 graden
Voor de richting van een vector mogen we de hoek nemen die een vector met de reële as maakt (draairichting linksom = positief).
Periodieke functies
Een periodieke functie is een functie die periodiek (per periode) dezelfde waarden aanneemt zoals sin(x) of cos(t). We kunnen een periodieke functie in het complexe vlak voorstellen als een ronddraaiende vector.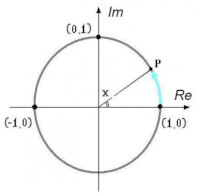 -fig 3- / Bron: Tronic
-fig 3- / Bron: TronicAls we bekijken welk complex getal de vector telkens aanwijst, dan vinden we de uitdrukking: z = re + j im = cos(ωt) + j sin(ωt)
Zie figuur 3, een andere schrijfwijze voor dit complexe getal is:
- exp (jx) = cos(x) + j sin(x)
- re [exp (jx)] = cos(x)
- im [exp (jx)] = sin(x)
Uitgebreide schrijfwijze:
- exp(a + jb) = exp(a) (cos(b) + j sin(b))
Tweedegraads vergelijkingen
 -fig 5- / Bron: Tronic
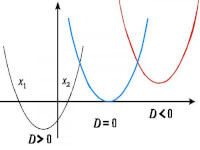
-fig 5- / Bron: Tronic- ax² + bx + c = 0
Deze vergelijking heeft ,voor getallen uit R2, twee mogelijke oplossingen voor x, een mogelijke oplossing voor x, of geen oplossing mogelijk. Dit nt .
- x1,2 = (-b ± √ D ) / 2a, D (=b²- 4ac)
- (D>0) -- de vergelijking heeft 2 oplossingen (x1 en x2)
- (D=0) -- één oplossing voor x
- (D<0) -- geen oplossing.
Voor de verzameling getallen uit de verzameling C -alle complexe getallen- heeft de tweedegraadsvergelijking complexe oplossingen als (D<0), deze oplossingen zijn:
x1,2 = (-b ± j√d ) / 2a
(√D = ± j√d )bijvoorbeeld:
2x² + x + 1 = 0
√D = √(b²- 4ac) = √(1-8) = √(-7) = ± j√7
x1,2 = (-1 ± j√7) / 4
voorbeeld gedempte trilling (periodiek signaal)
Op een seriegeschakelde spoel L, capaciteit C, en weerstand R wordt een constante spanning U aangesloten. De vergelijking voor de stroom door de componenten is:
i * R + L (di/dt) + 1/C ∫ ic dt = U
i (R + sL + 1/sC) = U
ω = 1/√(LC)
Ω = R/2L
i (s² + 2Ωs + ω²) = s/L U
 -fig 4- / Bron: Tronic
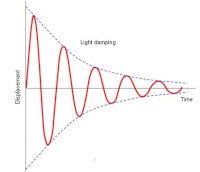
-fig 4- / Bron: Tronici (s² + 2Ωs + ω²) = 0
Afhankelijk van de waarden van Ω en ω heeft deze vergelijking verschillende typen oplossingen. Voor Ω < ω zal de oplossing voor deze vergelijking een gedempte trilling zijn.
De stroomfunctie ziet er zo uit:
- i(t) = exp(-Ωt) [C sin(ωt) + D cos(ωt)]