Wiskunde: verzamelingen van de getallen
 Getallen worden overal voor gebruikt. Zonder getallen waren we nergens gekomen. De wiskunde is sterk afhankelijk van getallen. Ze zijn er in alle soorten en maten. Positieve getallen, negatieve getallen, gehele getallen, breuken en ga zo maar door. De wiskunde heeft een mooie indeling gemaakt die de getallen opdeelt in verschillende verzamelingen die elk weer deel zijn van elkaar. Dit is mooi weer te geven in een venndiagram. Elke verzameling van getallen heeft zijn eigen toepassingen binnen de wiskunde.
Getallen worden overal voor gebruikt. Zonder getallen waren we nergens gekomen. De wiskunde is sterk afhankelijk van getallen. Ze zijn er in alle soorten en maten. Positieve getallen, negatieve getallen, gehele getallen, breuken en ga zo maar door. De wiskunde heeft een mooie indeling gemaakt die de getallen opdeelt in verschillende verzamelingen die elk weer deel zijn van elkaar. Dit is mooi weer te geven in een venndiagram. Elke verzameling van getallen heeft zijn eigen toepassingen binnen de wiskunde.
Getallen
Getallen zijn objecten met een waarde. Hoeveel ze waard zijn hangt af van de grootte van het getal. We kunnen getallen opdelen in een aantal verzamelingen. Deze verzamelingen worden vaak weergegeven in de vorm van een venndiagram. Dit is een diagram waarin de kleinste verzameling in het midden staat. Daaromheen zit de een na kleinste verzameling. De kleinste verzameling is bevat in de een na kleinste verzameling. Je zou dus kunnen zeggen dat de een na kleinste verzameling een uitbreiding is van de kleinste verzameling. Om deze verzameling zit weer een grotere verzameling en zo ga je door totdat je alle getallen hebt.Verzamelingen van getallen
Natuurlijke getallen
De natuurlijke getallen worden normaliter gezien als kleinste verzameling getallen. Ze bestaan uit alle gehele getallen groter dan nul. Over of nul zelf ook een natuurlijk getal is zijn de meningen verdeeld. Informatici claimen vaak van wel. Wiskundigen neigen vaak naar nee, maar ook dat is niet altijd waar. Het maakt in principe niet veel uit of nul wel of niet bij de natuurlijke getallen wordt gerekend. Er zijn oneindig veel natuurlijke getallen. Dit is vrij eenvoudig te bewijzen op de volgende manier:Stel er zijn eindig veel natuurlijke getallen. Dan moet er een of meerdere de grootste zijn. Noem dit element k. Maar k+1 is groter dan k en voldoet ook aan de definitie van een natuurlijk getal. Dus k was niet de grootste. Dit is een tegenspraak, dus er zijn oneindig veel natuurlijke getallen.
De natuurlijke getallen komen vaak voor in de wiskunde. Telproblemen zijn een voorbeeld van een tak binnen de wiskunde die voornamelijk met de natuurlijke getallen rekent.
Gehele getallen
De eerste uitbreiding op de natuurlijke getallen is de verzameling van de gehele getallen. Deze bestaat uit alle gehele getallen, dus positief en negatief. Nul hoort hier zeker ook bij. Ook dit zijn er oneindig veel. Het zijn er ook precies evenveel als de natuurlijke getallen. Dit klinkt misschien raar maar dit is te bewijzen op de volgende manier:Als we een afbeelding kunnen maken die elk geheel getal op een natuurlijk getal afbeeldt, en we hebben voor alle gehele getallen een uniek natuurlijk getal, dan moeten het er wel evenveel zijn. Maak de afbeelding die 0 afbeeldt op 0, 1 op 1, -1 op 2, 2 op 3, -2 op 4 enzovoort. Dus het moeten er precies evenveel zijn.
De gehele getallen worden vaak gebruikt bij het modulorekenen. Als je modulo n rekent reken je op veelvouden van n na. Zo is 15 bijvoorbeeld gelijk aan 7 modulo 8, want 15 = 7 + 1 * 8. 23 = 7 + 2 * 8 dus ook 23 is modulo 8 gelijk aan 7.
Quotiënten
De quotiënten, ofwel breuken, zijn alle getallen die bestaan uit een deling van twee gehele getallen. Ook dit zijn er weer precies evenveel als natuurlijke getallen en gehele getallen. Dit is op een gelijkwaardige manier aan te tonen. Je kunt de breuken namelijk ordelijk opschrijven als: 1/1, 1/2, 2/1, 3/1, 2/3, 1/3, 1/4, 2/4, 3/4, 4/4 enzovoort. Op deze manier maak je als het ware een slinger door alle breuken en weet je zeker dat je ze allemaal hebt gehad. Ken nu aan elke breuk een natuurlijk getal toe en je bent er. Breuken zijn veelgebruikt binnen de wiskunde. Bijvoorbeeld de kansrekening heeft heel veel te maken met de quotiënten.Reële getallen
De verzameling van reële getallen bestaat uit alle breuken, en alle getallen die niet als breuk te schrijven zijn. Dit worden ook wel transcendente getallen genoemd. Voorbeelden hiervan zijn pi en e. Deze verzameling bestaat ook weer uit oneindig veel elementen, maar deze keer zijn het er meer dan bij de breuken, gehele en natuurlijke getallen. Het is namelijk niet mogelijk om een dergelijke afbeelding te maken, zoals dat bij de andere verzamelingen wel kon. Je kunt de reële getallen namelijk niet in een ordelijke volgorde zetten op een dusdanige manier dat je ze allemaal hebt. De reële getallen komen in bijna alle takken van de wiskunde voor. Pi en e zijn twee belangrijke getallen die in veel wiskundige problemen terugkeren.Complexe getallen
Een complex getal bestaat uit een reëel deel en een imaginair deel. Alle reële getallen zitten hier dus bij. Zij hebben imaginair deel nul. Het imaginaire deel bestaat uit een reëel getal maal i. Het getal i is een imaginair getal. Het is een getal waarvan het kwadraat -1 is. Oftewel i is de wortel van -1. In de reële getallen kunnen we geen wortel van een negatief getal nemen, maar dit kan bij de complexe getallen dus wel. De complexe getallen zijn ontstaan toen men naar een algemene formule zocht voor het oplossen van derdegraads vergelijkingen. Op een gegeven moment hadden ze die gevonden, alleen kwamen er soms 'onzinantwoorden' uit. Op dat moment zijn mensen betekenis gaan hechten aan deze getallen, en uiteindelijk bleek dat de complexe getallen nog veel meer toepassingen hadden. Zo kunnen de complexe getallen bijvoorbeeld gebruikt worden om bepaalde integralen op te lossen die zonder complexe getallen ongelofelijk moeilijk of zelfs onmogelijk uit te rekenen zijn. Verder kunnen de complexe getallen ook gebruikt worden voor het oplossen van bepaalde meetkundige problemen. En er zijn nog veel meer toepassingen.Lees verder
© 2017 - 2025 Gujanator, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
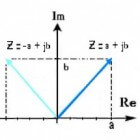 Complexe getallenIn het dagelijks leven rekenen we met getallen uit de reële verzameling R. Complexe getallen, of getalparen, zijn een ui…
Complexe getallenIn het dagelijks leven rekenen we met getallen uit de reële verzameling R. Complexe getallen, of getalparen, zijn een ui…
 De getallenverzameling der natuurlijke getallenDeze verzameling getallen mag beschouwd worden als opgebouwd uit de eenvoudigste getallen die we kennen. Het zijn de get…
De getallenverzameling der natuurlijke getallenDeze verzameling getallen mag beschouwd worden als opgebouwd uit de eenvoudigste getallen die we kennen. Het zijn de get…
 Oplossen van vergelijkingen met de positieve gehele getallenEen wiskundige vergelijking bestaande uit positieve gehele getallen is een gelijkheid waarin een onbekende term x verwer…
Oplossen van vergelijkingen met de positieve gehele getallenEen wiskundige vergelijking bestaande uit positieve gehele getallen is een gelijkheid waarin een onbekende term x verwer…
 Goniometrie - theorie en voorbeeldenIn de technische wiskunde wordt veel gewerkt met vaardigheden zoals algebra en meetkunde. Zo moeten functies gelijk zijn…
Goniometrie - theorie en voorbeeldenIn de technische wiskunde wordt veel gewerkt met vaardigheden zoals algebra en meetkunde. Zo moeten functies gelijk zijn…
 Factoranalyse: de componentenanalyseFactoranalyse is een parapluterm voor verschillende multivariate analyses, die als doel hebben om meerdere afhankelijke…
Factoranalyse: de componentenanalyseFactoranalyse is een parapluterm voor verschillende multivariate analyses, die als doel hebben om meerdere afhankelijke…
Gerelateerde artikelen
Soorten getallenIn de wiskunde zijn verschillende soort getallen bekend. Deze soorten getallen hebben allen hun eigen eigenschappen. Zo…
Bronnen en referenties
- Inleidingsfoto: Geralt, Pixabay
Gujanator (35 artikelen)
Laatste update: 10-03-2017
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 1
Laatste update: 10-03-2017
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 1
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.