Hoe reken je het weerstandsmoment voor sterkte uit?
 Om de sterkte van een balk te kunnen uitrekenen moet worden nagegaan in hoeverre het weerstandsmoment voldoet. Ieder vorm en ieder profiel heeft deze zogeheten W-waarde en is afgeleid van de I-waarde oftewel het traagheidsmoment van de doorsnede. Die waarde wordt gebruikt om de mate van doorbuiging te bepalen, terwijl de W-waarde de feitelijke draagcapaciteit bepaalt (wordt de doorsnede meer belast dan het aan kan zal de constructie feitelijk kapot gaan). Hoe wordt de W-waarde van een doorsnede bepaald en hoe wordt het verder afgeleid?
Om de sterkte van een balk te kunnen uitrekenen moet worden nagegaan in hoeverre het weerstandsmoment voldoet. Ieder vorm en ieder profiel heeft deze zogeheten W-waarde en is afgeleid van de I-waarde oftewel het traagheidsmoment van de doorsnede. Die waarde wordt gebruikt om de mate van doorbuiging te bepalen, terwijl de W-waarde de feitelijke draagcapaciteit bepaalt (wordt de doorsnede meer belast dan het aan kan zal de constructie feitelijk kapot gaan). Hoe wordt de W-waarde van een doorsnede bepaald en hoe wordt het verder afgeleid?
Weerstandsmoment uitrekenen
Weerstandsmoment voor sterkte
Het traagheidsmoment vormt binnen de elastische mechanica een belangrijke eenheid om mee te rekenen, omdat daarmee de doorbuiging van liggers wordt bepaald. De constructie wordt namelijk belast met representatieve belasting en dat leidt tot een vervorming. Daarnaast moet de constructie ook voldoen aan de sterkte, welke wordt gebaseerd op rekenbelasting en het weerstandsmoment. Deze twee worden als volgt berekend:- doorbuiging = δ = Mrep * L^2 / (48 * E * I) met daarin E is elasticiteit en L is de lengte;
- sterkte = σ = Md / Wd ≤ σd;
- I-waarde: is een tot de vierde macht uitkomst dat wordt uitgedrukt in mm^4 als eenheid;
- W-waarde: is een tot de derde macht uitkomst dat wordt uitgedrukt in mm^3.
Rechthoek en vierkant
Bij een rechthoek of vierkant is er sprake van een breedte en een hoogte, waarbij bij de vierkant de maten gelijk aan elkaar zijn. Er is dus sprake van de gekwadrateerde afstand naar het aangrijpingspunt vermenigvuldigd met het oppervlak. Oftewel er is sprake van r^2*dA. Integreren we die beschouwing dan wordt het volgende gevormd:- ∫ r^2*dA waarbij over de hoogte wordt geïntegreerd, wat praktisch inhoudt;
- b*∫ (h)^2*dh = b*1/3*h^3 (over 1/2*y tot -1/2*y) = b/3*[(1/2*h)^3-(-1/2*h)^3] = b/3*[1/8*h^3+1/8*h^3];
- b/3*1/4 *h^3 (b blijft over van het oppervlak, aangezien naar h is geïntegreerd;
- I rechthoek = 1/12 *b*h^3;
- I vierkant = 1/12 *h^4 (b=h).
Om de W-waarde te bepalen dient de zojuist bepaalde waarde te delen door de halve hoogte oftewel:
- W rechthoek = 1/12 *b*h^3 / (1/2*h) = 1/6 * b*h^2;
- W vierkant = 1/6 *h^3.
Driehoek
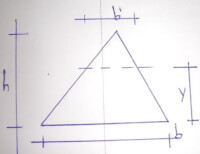 Bron: Http://geinformeerd.infoteur.nl
Bron: Http://geinformeerd.infoteur.nl- b’ = breedte op hoogte h = b * (1-y/h) waarin y de afstand is tot de basislijn;
- Ip = ∫y^2*dA = ∫y^2*b*(1-y/h)*dy = b*[1/3*y^3-1/4*y^4/h] over 0 tot h = b*[1/3*h^3-1/4*h^3].
Op de basislijn zou gelden:
- Ip driehoek = 1/12 *b*h^3 echter de driehoek dient nog naar het evenwichtspunt worden verplaatst waardoor een correctie op de I waarde volgt van:
- I driehoek = 1/12 *b*h^3 – A*r^2;
- I driehoek = 1/12 *b*h^3 – ½ *b*h*(1/3*h)^2 = 1/12 * b*h^3 – 1/18 *b*h^3 = 1/36 *b*h^3.
Om de W-waarde te bepalen kan worden gebruik gemaakt van de afstand tot de boven en onderkant:
- W driehoek onder = 1/36 *b*h^3 / (1/3*h ) = 1/12 *b*h^2;
- W driehoek boven = 1/36 *b*h^3 / (2/3*h) = 1/24 *b*h^2.
Cirkel en buis
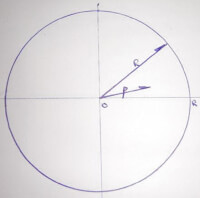 Bron: Http://geinformeerd.infoteur.nl
Bron: Http://geinformeerd.infoteur.nl- A = oppervlak = π*r^2 = ¼*π*d^2;
- Ip-cirkel = Ix-richting + Iy-richting = ∫ x^2*dA + ∫ y^2*dA = polair traagheidsmoment welke eerst moet worden bepaald;
- Ip = ∫ p^2*dA met dA = 2*π*p*dp met p = de straal over 0 tot r;
- Ip = ∫ p^2*2*π*p*dp = 2*π*[1/4*p^4] over 0 tot r = 2/4*π*r^4 = ½*π*r^4
De polaire I waarde vormt het moment in twee richtingen echter de I-waarde in 1 richting is benodigd, oftewel:
- Ix-cirkel = Iy = [½*π*r^4]/2 = ¼*π*r^4 in geval van een straal;
- Ix-cirkel = 1/64*π*d^4 in geval van een diameter (r^4= (1/2*d)^4= 1/16*d^4);
- Ix-buis = 1/64*π*(D^4-d^4) = ¼*π*(R^4-r^4);
- Wx-cirkel = Wy = Ix of Iy gedeeld door de halve afstand oftewel ½*d of r;
- Wx-cirkel = Wy = ¼*π*r^4 / r = ¼*π*r^3;
- Wx-cirkel = Wy = 1/64*π*d^4/(1/2*d) = 1/32*π*d^3.
- Wx-buis = 1/32*π*(D^4-d^4)/D = ¼*π*(R^4-r^4)/R.
Stelling van Steiner
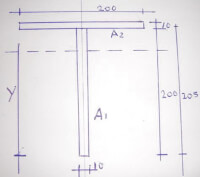 Bron: Http://geinformeerd.infoteur.nl
Bron: Http://geinformeerd.infoteur.nl- I samengesteld = I1 + A1*(y1-y)^2 + I2 + A2*(y2-y)^2;
- met een totaal oppervlak van A1 + A2;
- y = (A1*yA1 + A2*yA2) / (A1+A2);
- W samengesteld = I samengesteld / y.
Bij een T-balk profiel met lijf is 200 mm hoog, 10 mm dik met een flens daarop van 200 mm breed en 10 mm hoog geldt:
- y = neutrale lijn tot rand = (10*200*100+200*10*205)/(4000) = 152,5 mm;
- I1 = 1/12*10*200^3+200*10*(100-152,5)^2 = 12.179.167 mm^4;
- I2 = 1/12*200*10^3+10*200*(205-152,5)^2 = 5.529.167 mm^4;
- I totaal = 17.708.334 mm^4;
- W samengesteld = 17.708.334/152,5 = 116.120 mm^3.
Lees verder
© 2012 - 2025 Geinformeerd, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Ligging van neutrale lijn samengestelde ligger of oppervlakComplexe vormen bestaande uit vierkanten, ronde delen, uitstekende strips enzovoorts kunnen een constructief sterke vorm…
Ligging van neutrale lijn samengestelde ligger of oppervlakComplexe vormen bestaande uit vierkanten, ronde delen, uitstekende strips enzovoorts kunnen een constructief sterke vorm…
 Waarom hebben stalen liggers een bepaalde vorm?Liggers hebben tot doel om belasting over een opening te tillen tot het aansluitende vlak is bereikt. Het voorkomt dus d…
Waarom hebben stalen liggers een bepaalde vorm?Liggers hebben tot doel om belasting over een opening te tillen tot het aansluitende vlak is bereikt. Het voorkomt dus d…
 Omtrek berekenen van een wiskundig figuurHet komt regelmatig voor dat je moet weten wat de omtrek van iets is. Het is daarom handig om te weten hoe je de omtrek…
Omtrek berekenen van een wiskundig figuurHet komt regelmatig voor dat je moet weten wat de omtrek van iets is. Het is daarom handig om te weten hoe je de omtrek…
 Herleiden zwaartepunt rechthoek, driehoek, halve cirkelRonde vormen, driehoeken en vierkanten, we komen ze overal en altijd tegen. In bepaalde omstandigheden kan het nuttig of…
Herleiden zwaartepunt rechthoek, driehoek, halve cirkelRonde vormen, driehoeken en vierkanten, we komen ze overal en altijd tegen. In bepaalde omstandigheden kan het nuttig of…
 Hoe reken je dwarskrachtwapening van een balk uit?Betonbalken worden toegepast, omdat deze tegen een relatief gunstige prijs kwaliteit verhouding veel belasting kunnen op…
Hoe reken je dwarskrachtwapening van een balk uit?Betonbalken worden toegepast, omdat deze tegen een relatief gunstige prijs kwaliteit verhouding veel belasting kunnen op…
Gerelateerde artikelen
Het paradox van technologische ontwikkelingDe wereld om ons heen verandert met duizelingwekkende vaart. We leven in een soort science fiction film, waarin we binne…
Bronnen en referenties
- Inleidingsfoto: Fangol, Rgbstock
- http://nl.wikipedia.org/wiki/Stelling_van_Steiner
- http://nl.wikipedia.org/wiki/Traagheidsmoment
- http://nl.wikipedia.org/wiki/Weerstandsmoment
- Afbeelding bron 1: http://geinformeerd.infoteur.nl
- Afbeelding bron 2: http://geinformeerd.infoteur.nl
- Afbeelding bron 3: http://geinformeerd.infoteur.nl
Geinformeerd (1.029 artikelen)
Laatste update: 17-01-2020
Rubriek: Wetenschap
Subrubriek: Techniek
Bronnen en referenties: 7
Laatste update: 17-01-2020
Rubriek: Wetenschap
Subrubriek: Techniek
Bronnen en referenties: 7
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.