Straal cirkel door drie punten bepalen

Indien men het oppervlak en/of de omtrek van een cirkel weet, dan kan daaruit snel de straal worden achterhaald. Dit wordt anders als men door drie verschillende punten of coördinaten een cirkel moet maken. Het is daarbij de vraag wat de feitelijke straal is en waar het middelpunt ligt. Hoe kan op basis van drie coördinaten (oftewel lengte van de drie zijden is bekend) de straal van een cirkel worden bepaald?

Straal cirkel door drie punten bepalen

• Omtrek en oppervlak
• Basis en hoek
• Drie coördinaten vertalen naar afstand
• Straal cirkel bepalen met drie lengten

Omtrek en oppervlak

De omtrek van een cirkel is vastgelegd met de volgende relatie: O = 2*π*r = π*d met daarin r = straal, d = diameter en π = 3,14 (afgerond). Oftewel de diameter past 3,14 maal in de omtrek. Weet men de omtrek, dan kan daaruit direct de straal worden bepaald:

• r = O / (2*π) bij een O = 31,41 geldt r = 34,41 / (2*π) = 5;
• d = O / π geldt r = 34,41 / π = 10.

Het oppervlak van een cirkel wordt uitgedrukt in de volgende relatie: A = π*r^2 = ¼*π*d^2. Daarin is r de straal en d de diameter. Is het oppervlak bekend, dan kan uit deze vergelijking rechtstreeks de straal en diameter worden bepaald. Oftewel:

• r = √(A/π) bij een A = 78,53 geldt √(78,53/π) = √25 = 5;
• d = √(4*A/π) hierbij geldt √(4*78,53/π) = √100 = 10 = 2*5.

Basis en hoek

Indien men de lengte van de basis kent en de overige zijden zijn even lang, dan kan het worden bepaald met L/√3. Is slechts de basis en overliggende hoek bekend, dan geldt 2r = a/sinA = b/sinB = c/sinC. Oftewel:

• r = L/√3 bij een basislengte van L = 8,66 geldt r = 8,66/√3 = 5;
• r = a/(2*sinA) bij een a = 8,66 en A = 60° geldt r = 8,66 / (2*sin60°) = 5.

Maar wat moet men doen als men drie punten of coördinaten heeft?

Drie coördinaten vertalen naar afstand

Heeft men drie punten oftewel coördinaten, dan staat de straal van de cirkel vast. Het wordt daarbij bepaald door de onderlinge afstand tussen deze punten. Oftewel men moet de coördinaten vertalen naar de werkelijke tussenafstand. Stel punt A ligt op (x1,y1), punt B op (x2,y2) en punt C op (x3,y3) dan geldt voor de tussenafstand het volgende:

• lengte A-B = √[(x2-x1)^2+(y2-y1)^2];
• lengte A-C = √[(x3-x1)^2+(y3-y1)^2];
• lengte B-C = √[(x3-x2)^2+(y3-y2)^2].

Stel A ligt op (0,0), B ligt op (2,3) en C ligt op (4,5), wat zijn dan de verschillende lengten tussen de punten?:

• lengte A-B = √[(2-0)^2+(3-0)^2] = √13 = 3,60;
• lengte A-C = √[(4-0)^2+(5-0)^2] = √41 = 6,40;
• lengte B-C = √[(4-2)^2+(5-3)^2] = √8 = 2,82.

Omdat één zijde ten opzichte van de andere twee relatief lang is, gaat het om een langwerpig en platte driehoek. Dit zal resulteren in een relatief grote straal. Uiteraard kan men ook de lengte van de drie schuinen rechtstreeks opmeten, zodat men het direct in de volgende formule kan invullen.

Straal cirkel bepalen met drie lengten

Op basis van voorgaande lengten kan middels volgende formule de lengte van de straal worden bepaald.

• r = A*B*C / √[(A+B+C)*(A+B-C)*(A+C-B)*(B+C-A)];
• r = √13*√41*√8/√[(√13+√41+√8)*(√13+√41-√8)*(√13+√8-√41)*(√41+√8-√13)];
• r = 65,30 / √[12,84*7,18*0,03*5,62] = 16,56.

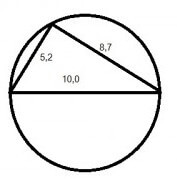
Stel men weet de volgende lengtes A = 5,2, B = 8,7 en C = 10 dan bedraagt de straal:

• r = 5,2*8,7*10 / √(5,2+8,7+10)*(5,2+8,7-10)*(5,2+10-8,7)*(8,7+10-5,2);
• r = 452,4 / √[23,9*3,9*6,5*13,5] = 452,4/90,4 = 5,00.

Door vanaf de drie punten de berekende straal te tekenen, vindt men bij het kruispunt het middelpunt van de cirkel. Trek daarna vanaf het gevonden middelpunt de straal, zodat de drie coördinaten worden gekruist.

Lees verder

• Bepalen zwaartepunt complexe figuren: statisch moment
• De booglengte van een kromme bepalen met Pythagoras
• Herleiden zwaartepunt rechthoek, driehoek, halve cirkel
• Hoe kun je de uitkomst van (a+b)^n gemakkelijk bepalen?