Afstanden berekenen in de sterrenkunde en kosmologie
 Iedereen kent wel het gezegde "meten is weten" en dit gaat zeker op in de sterrenkunde. Een afstand bepalen op het aardoppervlak is tegenwoordig met het gebruik van satellieten een eitje. Iedereen kan met zijn/haar computer of telefoon de afstand tussen twee willekeurige plaatsen op aarde in een mum van tijd te weten komen. Maar hoe meten sterrenkundigen de afstand tot andere sterren en sterrenstelsels? Hoe bepalen kosmologen de grootte van het universum? Welke meetlatten gebruiken zij voor hun afstandsbepalingen?
Iedereen kent wel het gezegde "meten is weten" en dit gaat zeker op in de sterrenkunde. Een afstand bepalen op het aardoppervlak is tegenwoordig met het gebruik van satellieten een eitje. Iedereen kan met zijn/haar computer of telefoon de afstand tussen twee willekeurige plaatsen op aarde in een mum van tijd te weten komen. Maar hoe meten sterrenkundigen de afstand tot andere sterren en sterrenstelsels? Hoe bepalen kosmologen de grootte van het universum? Welke meetlatten gebruiken zij voor hun afstandsbepalingen?Warning: Undefined array key 3 in /data/sites/web/interatenl/subsites/infonu.nl/include/config.inc.php on line 374
Warning: Undefined array key 4 in /data/sites/web/interatenl/subsites/infonu.nl/include/config.inc.php on line 374
Warning: Undefined array key 5 in /data/sites/web/interatenl/subsites/infonu.nl/include/config.inc.php on line 374
Warning: Undefined array key 6 in /data/sites/web/interatenl/subsites/infonu.nl/include/config.inc.php on line 374
Warning: Undefined array key 7 in /data/sites/web/interatenl/subsites/infonu.nl/include/config.inc.php on line 374
Inhoud
Spiegels op de maan
De afstand tot onze maan is tegenwoordig tot op een paar millimeter nauwkeurig te meten. Tijdens de Apollo missies van 1969-1972 hebben de astronauten drie maanspiegels/retroreflectoren op het oppervlak van de maan geplaatst. Nu kan men vanaf de aarde een laserstraal op zo een spiegel richten (wat grote deskundigheid vereist). De laserstraal zal door de maanspiegel/reflector teruggekaatst worden. Door de tijd te meten die de lichtstraal erover heeft gedaan om van de aarde naar de maan te komen en weer terug en deze te delen door de lichtsnelheid kan men de afstand berekenen. Nu hebben sterrenkundigen deze meting de afgelopen decennia regelmatig uitgevoerd en zijn tot de ontdekking gekomen dat de maan zich van de aarde verwijdert met 38 millimeter per jaar.Kosmologische meetlatten
Omdat het universum zo onvoorstelbaar groot is hebben sterrenkundigen/kosmologen verschillende meetmethoden ontwikkeld voor verschillende meetdoeleinden. Een zogenaamde kosmische ladder waarvan de eerste trede ons eigen zonnestelsel is. Objecten binnen ons eigen zonnestelsel worden voornamelijk gemeten door middel van radarmeting. Voor afstandsberekeningen tot nabijgelegen sterren en sterren binnen ons melkwegstelsel wordt gebruik gemaakt van de klassieke driehoeksmeting ofwel de parallaxmethode. Gaan we metingen verrichten buiten ons zonnestelsel dan hebben sterrenkundigen weer andere meetmethoden ontwikkeld. Men moet wel in gedachte houden dat de nauwkeurigheid van deze meetmethoden wel minder wordt. Een veel gebruikte methode om de afstand te bepalen van sterren in een ander sterrenstelsel zijn Cepheïden ofwel standaardkaarsen. Zijn deze echter niet aanwezig in een sterrenstelsel dan kan men gebruik maken van roodverschuiving. Roodverschuiving kan men gebruiken voor zowel sterren als ook sterrenstelsels. De laatste trede van de kosmische ladder gebruikt men om de grootte en/of vergroting van de kosmos in zijn geheel te meten. Hiervoor maakt men gebruik van de kosmologische roodverschuiving.Radarmeting
Afstandsbepaling door middel van radarmeting werkt gelijk aan de bovenstaande beschrijving van de spiegels op de maan. Men zend een radarpuls richting het te meten hemelobject. Hierna vangt met het gereflecteerde signaal weer op en kan men de afstand berekenen door de tijd te meten tussen versturen en ontvangen. Radarpulsen reizen ook met de lichtsnelheid.Parallaxmethode
De basis voor de parallaxmeting is het kennen van de afstand van de aarde tot de zon, de astronomische eenheid of AE en het meten van de positie van een ster in onze melkwegstelsel op een bepaalde datum. De meting wordt een half jaar later herhaald. Omdat de aarde om de zon draait zien we bij de tweede meting de ster vanuit een net iets andere richting. Uit dit positieverschil (een fractie van een boogseconde) kan men de afstand berekenen van de ster tot de zon. De afstand van de gemeten ster wordt over het algemeen in parsec weergegeven. De parallaxmeting is te gebruiken voor sterren tot een afstand van een 1600 honderd lichtjaar en is vrij nauwkeurig. Nieuwe technieken zoals aan boord van de satelliet Gaia kunnen parallaxen met een nauwkeurigheid van 10 microboogseconden meten, sterren op een afstand tot enkele tienduizenden lichtjaren.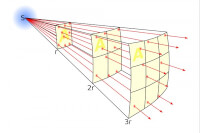 Omgekeerde kwadratenwet voor straling uit een puntbron / Bron: Borb, Wikimedia Commons (CC BY-SA-3.0)
Omgekeerde kwadratenwet voor straling uit een puntbron / Bron: Borb, Wikimedia Commons (CC BY-SA-3.0)Cepheïden
Cepheïden zijn zeldzame, zeer heldere sterren die met grote regelmaat van helderheid veranderen. Ze zijn genoemd naar δ Cephei, een met het blote oog zichtbare ster in het sterrenbeeld Cepheus waarbij deze helderheidsverandering voor het eerst is vastgesteld. Cepheïden zijn van andere veranderlijke sterren te onderscheiden door hun karakteristieke lichtkromme. Er is ontdekt dat de helderheidsverandering van Cepheïden afhankelijk is van hun gemiddelde lichtkracht. Heldere Cepheïden variëren veel trager van helderheid dan zwakke exemplaren. In nabijgelegen sterrenstelsels zijn afzonderlijke Cepheïden aan hun lichtkromme te herkennen. Door hun helderheidsverandering te meten, weet je hun gemiddelde lichtkracht. Door die te vergelijken met de waargenomen helderheid kan de afstand berekend worden. Dit soort sterren kunnen dus als standaardkaarsen dienen en zijn in overeenstemming met de omgekeerde kwadratenwet.Supernova type Ia & RR Lyrea sterren
De Omgekeerde kwadraten wet is ook van toepassing op:
- Supernova type Ia kan men ook gebruiken als een soort standaardkaars omdat dit soort type supernova vrijwel altijd dezelfde helderheid hebben.
- RR Lyrae sterren zijn pulserende variabele sterren met een regelmatige periode en dus ook als standaardkaars te gebruiken.
- Superreuzen (de grootste soort sterren) worden gebruikt om afstanden te bepalen van sterrenstelsels en elliptische sterrenstelsels op zeer grote afstand. In elliptische sterrenstelsels komen namelijk geen Cepheïden voor en in sterrenstelsels op grote afstand zijn ze vaak niet waarneembaar.
Roodverschuiving
Wanneer er geen standaardkaarsen meer bruikbaar zijn in verre sterrenstelsels kan men gebruik maken van het mechanisme roodverschuiving. Roodverschuiving is het Dopplereffect toegepast op de golfbeweging van licht. Roodverschuiving ontstaat door een uitdijend heelal. Hoe langer de lichtgolven door de uitdijende ruimte reizen, hoe sterker ze worden uitgerekt. Het licht van verre sterrenstelsels komt daardoor met een iets langere golflengte (roder) op aarde aan dan het licht van dichterbij gelegen stelsels. Wanneer men licht opvangt van een ver sterrenstelsel dan kan men hiervan het spectrum analyseren. In het spectrum van waterstof wordt een bepaalde spectraallijn waargenomen. Door te meten hoever die spectraallijn naar het rood is opgeschoven, volgt met het Dopplereffect de theoretische snelheid van het sterrenstelsel. Ook moet de evenredigheidsconstante tussen roodverschuiving en afstand nauwkeurig bekend zijn, de zogeheten Hubbleconstante. Met behulp van de Hubbleconstante en de grootte van de roodverschuiving is de afstand te berekenen (te schatten deze methode is niet super nauwkeurig).Kosmologische roodverschuiving
Door gebruik te maken van de roodverschuiving is gebleken dat sterrenstelsels zich van elkaar af bewegen. Vanaf de aarde gezien blijkt bij toenemende afstand ook dat ze met toenemende snelheid zich van ons af bewegen (de zogenaamde vluchtsnelheid). Deze sterrenstelsels bewegen zich dus met toenemende snelheid van ons af. Sterrenstelsels met snelheden die de snelheid van het licht benaderen zijn voor ons op aarde niet meer zichtbaar. De afstand waarbij de snelheid van sterrenstelsels gelijk is aan de lichtsnelheid bepaalt de kosmische horizon waarbuiten er voor ons geen waarnemingen te doen zijn. De afstand tot onze kosmische horizon is op dit moment ongeveer 50 miljard lichtjaar. Dus 50 miljard x 9,46 biljoen kilometer!Appendix
Astronomische eenheid of AEOnder astronomische eenheid wordt de gemiddelde afstand van de aarde tot de zon bedoeld en bedraagt 149,6 miljoen kilometer. In september 2012 is de Astronomische eenheid op exact 149.597.870.700 meter gezet.
Lichtsnelheid
De lichtsnelheid is de enigste constante in het universum. De snelheid van het licht in een vacuüm is 299.792.458 meter per seconde en wordt meestal afgerond op 300.000 kilometer per seconde.
Lichtjaar
Met een lichtjaar wordt de afstand bedoeld dat licht overbrugt in een periode van één jaar volgens de aardse kalender. Deze afstand bedraagt 9.460.730.472.580.800 meter, afgerond 9,46 biljard meter ofwel 9,46 biljoen kilometer.
Parsec
De parsec is afgeleid van de parallaxmeting. 1 parsec = 3,262 lichtjaar en komt overeen met een parallax van 1 boogseconde.
Omrekenen
Hierbij een overzicht voor het omrekenen van de verschillende eenheden:
- 1 AE = 149 597 870 700 meter
- 1 AE = 8,317 lichtminuten
- 1 AE = 499 lichtseconden
- 1 lichtjaar = 63 241 AE
- 1 parsec = 206 265 AE
- 1 parsec = 3,262 lichtjaar