Hoe wordt een betonkolom doorgerekend?
 Indien beton als kolom in een gebouw wordt toegepast heeft het altijd een zeer belangrijke functie. Gewicht van boven uit de vloeren, het dak en wanden worden geconcentreerd afgevoerd. Oftewel er is altijd een hoge spanning aanwezig in de kolom. Het kan eveneens voorkomen dat de kolom wordt belast met een combinatie van normaal druk en een moment. Hoe kan het worden afgewapend en hoeveel moment kan het opnemen?
Indien beton als kolom in een gebouw wordt toegepast heeft het altijd een zeer belangrijke functie. Gewicht van boven uit de vloeren, het dak en wanden worden geconcentreerd afgevoerd. Oftewel er is altijd een hoge spanning aanwezig in de kolom. Het kan eveneens voorkomen dat de kolom wordt belast met een combinatie van normaal druk en een moment. Hoe kan het worden afgewapend en hoeveel moment kan het opnemen?Betonkolom uitrekenen
- Wat is het doel van een betonkolom?
- Achtergrond
- Uitsluiten van 2e orde effecten
- Excentriciteitseisen
- Ontwerpen via TBG 10.2.c tabel
- Een voorbeeld berekening
- Hoeveel kan het nu werkelijk opnemen?
Wat is het doel van een betonkolom?
De betonkolom heeft een belangrijke functie. Enerzijds kan het esthetisch een belangrijk onderdeel van een ruimte zijn en anderzijds dient het veel gewicht van boven naar beneden af te voeren. Het zorgt voor structurele veiligheid in een gebouw, waartoe de kolom voldoende wapening moet hebben. Het kan op twee manieren worden berekend door daartoe de GTB tabellen te gebruiken of te controleren hoeveel moment een afgewapende kolom werkelijk kan opnemen.Achtergrond
Indien een kolom simpel wordt belast op druk dan bestaat de kans dat door enige scheefstand een moment in de kolom wordt geïntroduceerd. Het heeft de neiging om uit te knikken. Vaak betreft het dan een standaard kolom, waarbij het geïntroduceerde moment dermate klein is dat er slechts standaard wapening benodigd is. Dit wordt anders indien er een moment koppeling aanwezig is. In dat geval neemt de kniklengte af echter het moment in combinatie met de drukbelasting dient overgedragen te worden. Hoe kan dit worden benaderd?Uitsluiten van 2e orde effecten
Een belangrijk aspect van de kolom is dat 2e orde effecten worden uitgesloten. De kolom mag slechts uitknikken ten gevolge van de erop staande belastingen en niet dat de slankheid aanleiding is voor aanvullende vervormingen. Oftewel het moet blijven bij de incidenteel optredende vervorming, waarvan de belastingen bekend zijn. Het benodigde oppervlak van een betondoorsnede is vaak minimaal:- 1 tot 1,5 maal N’d / f’b met daarin N’d = normaaldrukkracht en f’b de rekenwaarde drukcapaciteit van beton. De factor anderhalf wordt toegepast indien er grote momenten op de kolom staan.
Uitgangspunt van het tweede orde effect wordt gevonden door de verhouding tussen optredende en opneembare spanningen in een slanke doorsnede. Oftewel:
- αn = N’d / (Ab*f’b) met Ab is het oppervlak van de doorsnede. Hieraan gekoppeld zijn de slankheidseisen;
- λh ≤ 5 / √αn indien αn ≤ 0,25;
- λh ≤ 10 indien 0,25 < αn ≤ 0,50;
- λh ≤ 15 – 10 * αn indien 0,50 < αn ≤ 1,00.
De slankheid λh wordt berekend door lc / h * f, waarin lc de lengte van de kolom is, h is de hoogte van de betondoorsnede en f een factor afhankelijk van methode van inklemming:
- gewone horizontale oplegging f = 1,0;
- toepassing van veer en veer (of moment boven naar moment onder) f = 0,8 (veelal van toepassing kolommen);
- toepassing van oplegging en inklemming f = 0,7;
- toepassing van veer en inklemming f = 0,6;
- tweemaal ingeklemd f = 0,5.
Is de slankheid werkelijk kleiner dan voorgaande eis dan kan treden 2e orde effecten niet op.
Excentriciteitseisen
Aanvullend gelden er eisen aangaande de excentriciteit. Op de kolom komen belastingen voor, welke aanleiding tot excentriciteit kunnen zijn. Indien er bijvoorbeeld geen moment wordt geintroduceerd dan dient aan de minimum eisen te worden voldaan zijnde:- e0 = Md / N’d met Md is optredend maximale moment;
- e0 ≥ lc / 300 ≥10 mm;
- et ≥ 0,01 * h.
Voorgaande informatie wordt in combinatie met de belasting en opneembare spanning gebruikt als ingang van de TGB tabellen.
Ontwerpen via TBG 10.2.c tabel
De TGB tabellen zijn opgesteld om de ontwerper van betonkolommen een helpende hand te geven. De TGB maakt gebruik van de volgende grafiek ingang: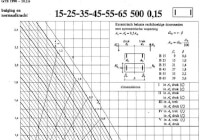 Bron: GTB-1990
Bron: GTB-1990 Bron: GTB-1990
Bron: GTB-1990- N’d / (Ab*f’b) vertikaal en horizontaal N’d / (Ab*f’b) * et/h. Dit laatste introduceert dus de theoretische excentriciteit van de kolom als opzoek parameter in de tabellen.
Hiermee kunnen een aantal gegevens uit de tabel worden gehaald. De schuin lopende lijnen vertegenwoordigen het wapeningspercentage dat in de kolom aanwezig moet zijn om de belasting in combinatie met excentriciteit op te nemen. Dit is de r-waarde welke nog met β moet worden gecorrigeerd afhankelijk van het toegepaste beton. Verder kun je op de tabel een aantal gegevens vinden, waarmee één en ander uitgerekend kan worden:
- As;ben = w0t * Ab/100;
- w0t = het toe te passen wapeningspercentage = r*β;
- β = correctiefactor afhankelijk van betonkwaliteit. Deze start op 0,6 bij C15 en neemt per betonklasse 0,4 toe. C25 is dus 1,0 en C35 is dus 1,4;
- r = het wapeningspercentage in percentages echter is nog ongecorrigeerd.
Een voorbeeld berekening
Stel we hebben een vierkante betonkolom 300 mm maal 400 mm en 3000 mm hoog. De kolom wordt gemaakt van betonkwaliteit van C25 en betonstaal FeB500. Er komt een normaalkracht in van 800 kN, waarnaast het maximale moment 250 kNm bedraagt. Hoeveel wapening is dan benodigd?:- Ab = 1,5 * 800.000/15 = 80.000 mm2;
- Ab toegepast = 300*400 = 120.000 mm2;
- αn = 1,5* 800.000 / ( 120.000*15 ) = 0,67;
- λh < 15 – 10*0,67 = 8,33;
- λh = 3000/400 * 0,80 = 6,00.
Er zullen geen tweede orde effecten optreden.
- e0 = Md/ N’d = 250.000.000/ 800.000 = 313 mm > 10 mm > 3000/300;
- et = 0,01*400 = 40 mm -> et = 313 mm;
- N’d / (f’b*Ab) = 800.000 / ( 15 * 300*400 ) = 0,44;
- N’d / (f’b*Ab) * et/h = 0,44*313/400 = 0,34.
Deze combinatie afgelezen in de grafiek geeft een r = 2,30. Daarmee wordt het volgende bepaald:
- w0t = r*β = 2,30 * 1,0 = 2,30% wapeningspercentage;
- As;ben = 2,30 * 300*400/100 = 2760 mm2;
- dit is 1380 mm2 per zijde van de kolom en komt overeen met 3 rond 25 per zijde ( 1473 mm2).
Hoeveel kan het nu werkelijk opnemen?
Uiteraard is het hierbij de vraag hoeveel de kolom nu werkelijk aan kan qua belasting. Hoe kun je op basis van de wapening bepalen hoeveel er werkelijk kan worden opgenomen?:- As;toegepast = 1473 mm2;
- Ns = As*fs = N’s = 1473 * 435 = 640.755 N aan staaltrek en –druk op te nemen (op 50 mm van boven en onderkant betonrand);
- N’b = betondrukvermogen = 3/4*b*xu*f’b = 3/4*300*xu*15 = 3375*xu;
- xu = 800.000/3375 = 237 mm;
- Mu = N’d*(1/2*h-7/18*xu)+Ns*a+N’s*’a = 800*(0,2-7/18*0,237)+2*640,755*0,15 = 278 kNm;
- UC;As = 1380/1473 = 0,93;
- UC;Md = 250/278 = 0,90.
Dat houdt in dat de beton kolom voldoet.
Voorgaande beschouwing zegt eveneens dat de ontwerpmethode via de GTB tabellen werkt en dat de momenten goed zijn afgewapend. Let wel de laatste controle hoeveel moment de kolom werkelijk kan opnemen binnen de GTB tabellen buiten beschouwing wordt gelaten.