T-toets 3 - gemiddelden afhankelijke steekproeven

Een t-toets derde variant wordt uitgevoerd om te kijken of een verschil tussen twee afhankelijke steekproeven significant verschillen. Oftewel: is er meer aan de hand dan toeval? Er kan bijvoorbeeld gekeken worden of een voormeting significant verschilt van een nameting. Wat wordt er bedoeld met ‘afhankelijke steekproeven’ en hoe bereken je of de gemiddelden significant verschillen?

T-toets derde variant: Gemiddelden van afhankelijke steekproeven vergelijken

Met afhankelijke steekproeven wordt bedoeld dat de waarden die gemeten worden elke keer bij dezelfde persoon horen. Dit is bijvoorbeeld het geval bij een voor- en nameting zoals vaak bij trainingen gedaan worden. Een vraag kan bijvoorbeeld zijn: hoeveel weegt u? Vervolgens wordt een dieet gevolgd, waarna dezelfde vraag nogmaals gesteld wordt aan dezelfde persoon. Zo ontstaan paren van gegevens. Daarom wordt deze toets ook wel t-toets voor gepaarde gegevens genoemd. Hieruit vloeit voort dat de steekproeven altijd hetzelfde aantal onderzoeksobjecten heeft. Bij een t-toets tweede variant kunnen de steekproeven even groot zijn, maar dat hoeft niet.

Vervolgens wordt gekeken of het verschil tussen de steekproeven dan ook significant is. Dus: ‘Heeft het dieet invloed op het gewicht?’ (tweezijdige toetsing) of ‘Zorgt het dieet voor een daling in gewicht?’ (eenzijdige toetsing).

De formule

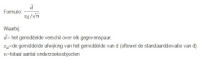
Voor het berekenen van het gemiddelde verschil over elk gegevenspaar:
Stap 1: Kijk naar je hypothese welke gegevens je van welke aftrekt (bij tweezijdige toetsing maakt dat niet uit)
Stap 2: Trek één voor één de paren van elkaar af
Stap 3: Tel alle uitkomsten op
Stap 4: Deel dit door het aantal metingen (n)

Vrijheidsgraden

Het aantal vrijheidsgraden wordt bij de T-toets eerste variant bepaald door het aantal meetwaarden min 1. Dit komt in formulevorm neer op:

Df = n-1

Df staat voor degrees of freedom.

Voorbeeld

Een onderzoeker wil weten of studenten op toets B beter zullen scoren dan op toets A. Daarvoor neem hij bij 15 studenten de toets af. De toetsen komen qua inhoud overeen en voor de toets kunnen maximaal 100 punten gehaald worden. De standdeviatie is 8,9 punten. Hij wil dit testen met een alfa van 1%.

Student	Cijfer toets A	Cijfer toets B
1	100	95
2	45	65
3	61	65
4	88	75
5	91	92
6	32	45
7	44	56
8	63	67
9	89	84
10	64	63
11	76	74
12	75	71
13	78	82
14	69	79
15	81	85

Nulhypothese: De studenten scoren evengoed of slechter op toets B dan op toets A
Alternatieve hypothese: De studenten scoren beter op toets B dan op toets A

Bereken vervolgens B-A per gegevenspaar (zie tabel).

Student	Cijfer toets A	Cijfer toets B	Verschil (B-A)
1	100	95	-5
2	45	65	20
3	61	65	4
4	88	75	-13
5	91	92	1
6	32	45	13
7	44	56	12
8	63	67	4
9	89	84	-5
10	64	63	-1
11	76	74	-2
12	75	71	-4
13	78	82	4
14	69	79	10
15	81	85	4
Gemiddelde	1056/15=70,4	1098/15=73,2	42/15=2,8

Nu het gemiddelde over de gegevensparen bekend zijn, is de formule in te vullen:

De gevonden t-waarde is 1,2185. De kritieke waarde bij df van 14 en een alfa van 1% is 2,624. Dit betekent dat de studenten niet significant beter scoren op toets B. Daardoor blijft de nulhypothese staan en wordt de alternatieve hypothese verworpen.

Lees verder

© 2013 - 2024 Marilyn, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.

Gerelateerde artikelen

Statistiek: Chi-kwadraat toetsMet de chi-kwadraat toets voor verdelingen (één variabele) en voor samenhang (twee variabelen) kun je uitrekenen of het…

De Chi-kwadraat toetsMet de Chikwadraattoets kun je bepalen of er een verband bestaat tussen twee variabelen. Deze toets is gebaseerd op een…

De Cito-toets oefenenDe Cito-toets in groep 8 bepaalt voor een groot deel naar welk niveau de kinderen zullen gaan op het voortgezet onderwij…

Wiskunde - de afgeleide en extreme waardesHoe bereken je de extreme waardes, ook wel minimum en maximum, en hoe stel je een raaklijn op? Vaak wordt dit gezien als…

Statistiek – Permutaties, Variaties en CombinatiesBij een kansberekening wil je weten welke kans er hoort bij een bepaalde gebeurtenis. Verschillende aspecten spelen hier…

Bronnen en referenties

Brinkman, J. (2007) Cijfers Spreken

Reactie

Ronald, 03-04-2015
Het verschil bij student 13 op toets A & B is niet 4 maar 16.
D wordt daardoor 3,6 i.p.v 2,8, nul hypothese blijft ook met dit juiste gemiddelde behouden. Reactie infoteur, 06-04-2015
Bedankt voor je oplettendheid!
Omdat het om een voorbeeld gaat, heb ik de waarden bij nummer 13 aangepast, zodat de rest nu ook klopt.

Marilyn (105 artikelen)
Laatste update: 06-04-2015
Rubriek: Wetenschap
Subrubriek: Wiskunde
Bronnen en referenties: 1

Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.

Student	Cijfer toets A	Cijfer toets B
1	100	95
2	45	65
3	61	65
4	88	75
5	91	92
6	32	45
7	44	56
8	63	67
9	89	84
10	64	63
11	76	74
12	75	71
13	78	82
14	69	79
15	81	85

Student	Cijfer toets A	Cijfer toets B
1	100	95
2	45	65
3	61	65
4	88	75
5	91	92
6	32	45
7	44	56
8	63	67
9	89	84
10	64	63
11	76	74
12	75	71
13	78	82
14	69	79
15	81	85

Student	Cijfer toets A	Cijfer toets B
1	100	95
2	45	65
3	61	65
4	88	75
5	91	92
6	32	45
7	44	56
8	63	67
9	89	84
10	64	63
11	76	74
12	75	71
13	78	82
14	69	79
15	81	85