Oplossen van polynomen - theorie en voorbeelden
 In veel beroepen wordt er gekeken naar polynomen. Wiskundigen stellen deze polynomen op om autoweggebruik in kaart te brengen, neerslag te meten of om de temperatuurschommelingen te onderzoeken. Tevens worden polynomen gebruikt om economische analyses te maken. Polynomen hebben zodoende een belangrijke positie in de wetenschap en het dagelijks leven. Zonder polynomen is de data die worden gebruikt in deze takken nietszeggend. Maar wat zijn polynomen en wat kan ermee gedaan worden?
In veel beroepen wordt er gekeken naar polynomen. Wiskundigen stellen deze polynomen op om autoweggebruik in kaart te brengen, neerslag te meten of om de temperatuurschommelingen te onderzoeken. Tevens worden polynomen gebruikt om economische analyses te maken. Polynomen hebben zodoende een belangrijke positie in de wetenschap en het dagelijks leven. Zonder polynomen is de data die worden gebruikt in deze takken nietszeggend. Maar wat zijn polynomen en wat kan ermee gedaan worden?- De polynoom
- Nuldegraads polynomen
- Eerstegraads polynomen
- Snijpunt met de y-as
- Snijpunt met de x-as
- Snijpunt met een andere grafiek
- Tweedegraads polynomen
- Snijpunt met de y-as
- Snijpunt met de x-as
- Snijpunt met een andere grafiek
De polynoom
Waar een functie op neerkomt is een aantal punten op een assenstelsel. Dit assenstelsel kan twee- (x,y), drie- (x,y,z) of vierdimensionaal (x,y,z,t) zijn. Indien deze punten op een bepaalde manier staan in het assenstelsel kunnen deze beschreven worden als een functie, een lijn waar deze punten op liggen. Dit kan een rechte, horizontale (of verticale) lijn zijn, een schuine lijn, een boog met een kantelpunt, een boog met twee kantelpunten enzovoort. Deze functies worden, uitgaande van een tweedimensionaal assenstelsel, genoemd naar hun aard:- Indien een lijn onveranderd horizontaal blijft is dit de nulde graad, zoals y = 1
- Indien een lijn constant verandert van y-positie naarmate x af- of toeneemt is dit een eerstegraads polynoom, zoals y = x - 3
- Indien een boog toe- of afnemend naar boven of beneden reist, omslaat en in de tegenovergestelde richting beweegt, is dit een tweedegraads polynoom, zoals y = -x2 + 2
Polynomen met toegenomen graden bestaan en worden gebruikt in Taylorreeksen. Een bekende Taylorreeks is die van sin(x). Deze wordt uitgedrukt als sin (x) ≈ x - (x3/3!) + (x5/5!) - (x7/7!) + (x9/9!)..., waarbij het uitroepteken een faculteit is. Dit betekent dat het getal wordt vermenigvuldigt met alle getallen die onder dat getal zitten, tot de nul. Zo wordt 3! uitgesproken als "drie faculteit" en is dit 3 * 2 * 1 = 6. Op dezelfde manier wordt 9! uitgesproken als "negen faculteit" en is de uitkomst 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 362880.
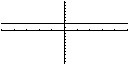 Figuur 1: f(x) = 2
Figuur 1: f(x) = 2Nuldegraads polynomen
Nuldegraads polynomen zijn grafieken waarbij de lijn onveranderd horizontaal blijft. Deze polynomen worden dikwijls gebruikt als raaklijn voor een andere grafiek. Een voorbeeld van een nuldegraads polynoom is f(x) = 2. Een oplossing voor f(x) = 0 is onmogelijk, omdat voor elke x de polynoom f(x) gelijk is aan 2. Dit is te zien in figuur 1. De lijn loopt horizontaal voor elke x en zodoende is elke oplossing die anders is dan 2 voor f(x) ongeldig.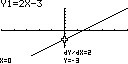 Figuur 2: f(x) = 2x - 3
Figuur 2: f(x) = 2x - 3Eerstegraads polynomen
Een eerstegraads polynoom is een polynoom is de vorm van f(x) = ax + b. Hierbij kunnen zowel a als b positieve of negatieve getallen zijn. Beschouw het voorbeeld f(x) = 2x - 3, zoals in figuur 2. In een eestegraads polynoom is de term a de richtingscoëfficiënt van de functie. De richtingscoëfficiënt bepaalt de richting van de grafiek. Indien de richtingscoëfficiënt positief is, zoals in het voorbeeld, dan zal de functie grotere getallen aannemen voor toenemende x. Invullen geeft weer hoe dit werkt. Indien er wordt gekozen dat de functie wordt geplot op x = 3 en x = 8, dan is f(3) = 2 * 3 - 3 = 3. Voor f(8) = 2 * 8 - 3 = 13. Omdat a positief is neemt de uitkomst van de functie toe naarmate de x toeneemt. Dit is een voorbeeld van een positieve richtingscoëfficiënt. Een negatieve richtingscoëfficiënt komt voor wanneer voor a een negatief getal wordt gekozen, waardoor de functie kleinere en negatieve getallen aanneemt naarmate x toeneemt. Dit betekent ook dat een functie kan snijden met een andere functie of aanwezigheid in het assenstelsel. Het snijpunt van een polynoom kan meerdere betekenissen hebben. Er kan namelijk gesneden worden met de x-as, de y-as of een andere functie. Aan de hand van enkele voorbeelden wordt elke situatie beschreven.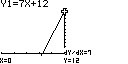 Figuur 3: f(x) = 7x - 12
Figuur 3: f(x) = 7x - 12Snijpunt met de y-as
In het geval van een snijpunt met de y-as dient er enkel 0 als x worden ingevoerd, daar op x = 0 de y-as staat. Voor f(x) = 7x + 12, afgebeeld in figuur 3, geldt zodoende dat op x = 0 het snijpunt met de y-as staat. De uitkomst is dan f(0) = 12. Het snijpunt van f(x) met de y-as is dan (0, 12). Op dezelfde manier geldt dat voor g(x) = 3x - 6 de uitkomst voor g(0) gelijk is aan -6. Oftewel, het snijpunt van g(x) met de y-as is (0, -6). De vuistregel is zodoende dat het snijpunt met de y-as van een functie f(x), in de vorm ax + b, gelijk is aan (0, b).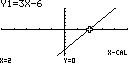 Figuur 4: f(x) = 3x - 6
Figuur 4: f(x) = 3x - 6Snijpunt met de x-as
Voor een snijpunt met de x-as dient de uitkomst van f(x) 0 te zijn, omdat op y = 0 de x-as aanwezig is. Ergo, f(x) = 7x + 12 moet gelijk zijn aan 0. Hieruit volgt dat 7x + 12 = 0. Aan beide zijden twaalf in mindering brengen geeft 7x = -12. Beide zijden delen door 7 geeft x = - 12/7. Oftewel, het snijpunt van f(x) met de x-as is (-12/7, 0). Op dezelfde manier geldt voor g(x) = 3x - 6 dat het snijpunt met de x-as zich bevindt op (2, 0). Dit is tevens te zien in figuur 4. Oftewel, voor snijpunten met de x-as van een functie f(x). in de vorm ax + b, bestaan de coördinaten uit (-b/a, 0).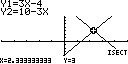 Figuur 5: de functies f(x) = 3x - 4 en g(x) = 10 - 3x snijden elkaar
Figuur 5: de functies f(x) = 3x - 4 en g(x) = 10 - 3x snijden elkaarSnijpunt met een andere grafiek
Beschouw de functies f(x) = 3x - 4 en g(x) = 10 - 3x. Deze grafieken snijden elkaar, alleen is nog niet duidelijk op welke positie dit gebeurt. Om het snijpunt te vinden moeten de grafieken gelijk zijn aan elkaar, zijnde f(x) = g(x). Door deze vergelijking op te lossen vindt men de x-coördinaat van het snijpunt. Deze x invullen in een van de (of beide) functies levert de y-coördinaat op.[OLIST]
Functies gelijk stellen aan elkaar. f(x) = g(x) → 3x - 4 = 10 - 3x
Termen met x naar een kant zetten, termen zonder x aan de andere kant zetten →6x = 14
Hieruit volgt x = 14/6
f(14/6) = 3, g(14/6) = 3
Hieruit volgt dat het snijpunt van f(x) met g(x) (en vice versa) zich bevindt op (14/6, 3), q.e.d. in figuur 5.
[/OLIST]
Functies gelijk stellen aan elkaar. f(x) = g(x) → 3x - 4 = 10 - 3x
Termen met x naar een kant zetten, termen zonder x aan de andere kant zetten →6x = 14
Hieruit volgt x = 14/6
f(14/6) = 3, g(14/6) = 3
Hieruit volgt dat het snijpunt van f(x) met g(x) (en vice versa) zich bevindt op (14/6, 3), q.e.d. in figuur 5.
[/OLIST]
Tweedegraads polynomen
Tweedegraads polynomen bestaan uit functies waarbij de hoogste macht die wordt geheven een twee is. Een voorbeeld van een dergelijke polynoom is de simpelste polynoom: f(x) = x2. Deze polynoom bestaat enkel uit de vorm f(x) = ax2, maar een tweedegraads polynoom kan ook de vorm f(x) = ax2 + c of f(x) = ax2 + bx + c aannemen. Strikt genomen bestaat elke polynoom uit de vorm f(x) = ax2 + bx + c, maar in het geval van f(x) = x2 betekent dit dat de termen b en c gelijk zijn aan 0. Dit is een feit dat relatief belangrijk is voor verdere berekeningen. Ook tweedegraads polynomen hebben namelijk snijpunten met de x- en y-assen, en met andere functies.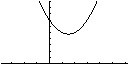 Figuur 6: f(x) = x2 - 3x + 7
Figuur 6: f(x) = x2 - 3x + 7Snijpunt met de y-as
Het snijpunt van een tweedegraads polynoom, en tevens van welke graad dan ook, met de y-as komt op hetzelfde neer als dat van een eerstegraads polynoom. Er hoeft simpelweg een 0 ingevuld te worden voor x om het snijpunt met de y-as te vinden. Beschouw het voorbeeld f(x) = x2 - 3x + 7, zie figuur 6. f(x) invullen met x = 0 geeft f(0) = 02 - 3 * 0 + 7 = 7. Hieruit volgt dat het snijpunt van f(x) met de y-as gelijk is aan (0, 7). Voor een tweedegraads polynoom geldt dus dat het snijpunt met de y-as gelijk is aan (0, c).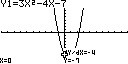 Figuur 7: p(x) = 3x2-4x-7. De grafiek raakt de x-as twee maal.
Figuur 7: p(x) = 3x2-4x-7. De grafiek raakt de x-as twee maal.Snijpunt met de x-as
Het snijpunt met de x-as voor een tweedegraads polynoom berekenen is een lastigere operatie. Voor een functie als f(x) = x2 lukt dit gemakkelijk, daar er geen lastige berekeningen hoeven te worden voldaan en de uitkomst dan (0, 0) is. Voor een polynoom zoals p(x) = 3x2-4x-7 of g(x) = 3x2-4x+7 wordt dit lastiger. In een dergelijk geval moet men gebruik maken van de discriminant. De discriminant wordt gebruikt om de x-coördinaten te berekenen waarbij de kwadratische functie 0 als resultaat geeft, en dus de x-as snijdt. Beschouw beide voorbeelden, waarbij het gebruik van de discriminant wordt afgebeeld.[OLIST]
Stel p(x) gelijk aan 0 → p(x) = 3x2-4x-7 = 0
Bereken de discriminant D van p(x) middels D = b2-4ac
D = (-4)2 - 4 * 3 * - 7 = 16 - - 84 = 100. Let hier op dat b altijd tussen haken staat om foute antwoorden te voorkomen.
Bereken vervolgens de x-coördinaten van de snijpunten volgens x = (-b ± √D) / 2a. Hieruit komen twee antwoorden.
x1 = (- - 4 + √(100)) / (2 * 3) = 14/6
x2 = (- - 4 - √(100)) / (2 * 3) = -1
Invullen in de functie geeft de volgende punten: (14/6, 0) en (-1, 0)
Oftewel, de snijpunten van p(x) met de x-as zijn (14/6, 0) en (-1, 0), zie figuur 7.
[/OLIST]
Stel p(x) gelijk aan 0 → p(x) = 3x2-4x-7 = 0
Bereken de discriminant D van p(x) middels D = b2-4ac
D = (-4)2 - 4 * 3 * - 7 = 16 - - 84 = 100. Let hier op dat b altijd tussen haken staat om foute antwoorden te voorkomen.
Bereken vervolgens de x-coördinaten van de snijpunten volgens x = (-b ± √D) / 2a. Hieruit komen twee antwoorden.
x1 = (- - 4 + √(100)) / (2 * 3) = 14/6
x2 = (- - 4 - √(100)) / (2 * 3) = -1
Invullen in de functie geeft de volgende punten: (14/6, 0) en (-1, 0)
Oftewel, de snijpunten van p(x) met de x-as zijn (14/6, 0) en (-1, 0), zie figuur 7.
[/OLIST]
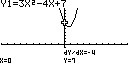 Figuur 8: g(x) = 3x2-4x+7 heeft geen snijpunten met de x-as.
Figuur 8: g(x) = 3x2-4x+7 heeft geen snijpunten met de x-as.[OLIST]
Stel g(x) gelijk aan 0 → g(x) = 3x2-4x+7 = 0
Bereken de discriminant D van g(x) middels D = b2-4ac
D = (-4)2 - 4 * 3 * 7 = 16 - 84 = -68.
Bereken vervolgens de x-coördinaten van de snijpunten volgens x = (-b ± √D) / 2a. Hieruit komen twee antwoorden.
x1 = (- - 4 + √(-68)) / (2 * 3) = geen antwoord
x2 = (- - 4 - √(-68)) / (2 * 3) = geen antwoord
De wortels van negatieve getallen hebben geen reële uitkomst, en zodoende snijdt deze functie de x-as niet.
[/OLIST]
Het is, zoals gedemonstreerd, ook mogelijk voor een functie om de x-as niet te raken. Zodoende is de discriminant handig om te berekenen of een kwadratische functie de x-as zal raken. Verder is de discriminant handig om met precisie te berekenen waar de functie de x-as zal raken. Een rekenmachine kan bijvoorbeeld een antwoord geven als x = 1,4142..., terwijl de discriminant een antwoord van √2 geeft.Stel g(x) gelijk aan 0 → g(x) = 3x2-4x+7 = 0
Bereken de discriminant D van g(x) middels D = b2-4ac
D = (-4)2 - 4 * 3 * 7 = 16 - 84 = -68.
Bereken vervolgens de x-coördinaten van de snijpunten volgens x = (-b ± √D) / 2a. Hieruit komen twee antwoorden.
x1 = (- - 4 + √(-68)) / (2 * 3) = geen antwoord
x2 = (- - 4 - √(-68)) / (2 * 3) = geen antwoord
De wortels van negatieve getallen hebben geen reële uitkomst, en zodoende snijdt deze functie de x-as niet.
[/OLIST]
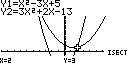 Figuur 9: f(x) = x2 - 3x + 5 en g(x) = 3x2 + 2x - 13 raken elkaar twee maal.
Figuur 9: f(x) = x2 - 3x + 5 en g(x) = 3x2 + 2x - 13 raken elkaar twee maal.Snijpunt met een andere grafiek
Het berekenen van het snijpunt van twee polynomen komt op hetzelfde neer als in het voorbeeld met de eerstegraads polynomen: stel ze aan elkaar gelijk en bereken de x-coördinaten van de snijpunten, waarna deze gebruikt kunnen worden om de y-coördinaten te berekenen. Neem als voorbeeld f(x) = x2 - 3x + 5 en g(x) = 3x2 + 2x - 13.[OLIST]
Stel f(x) gelijk aan g(x) → x2 - 3x + 5 = 3x2 + 2x - 13
Het verschil tussen deze functies moet 0 zijn om een snijpunt te creëren. Breng alle termen naar één kant.
(x2 - 3x2) + (- 3x - 2x) + (5 + 13) = 0
-2x2- 5x - 18 = 0
Gebruik discriminant D, hieruit volgen twee antwoorden.
D = b2 - 4ac
D = (- 5)2 + 4 * -2 * -18 = 25 + 144 = 169
x1 = (- - 5 + √(169)) / (2 * -2) = (5 + 13) / -4 = -18/4
x2 = (- - 5 - √(169)) / (2 * -2) = (5 - 13) / -4 = 8/4
Invullen in één van (of beide) grafieken geeft f(-18/4) = 155/4, g(-18/4) = 155/4
Verder geeft f(8/4) = 3, g(8/4) = 3
Ergo, de snijpunten zijn (-18/4, 155/4) en (2, 3)
[/OLIST]
Stel f(x) gelijk aan g(x) → x2 - 3x + 5 = 3x2 + 2x - 13
Het verschil tussen deze functies moet 0 zijn om een snijpunt te creëren. Breng alle termen naar één kant.
(x2 - 3x2) + (- 3x - 2x) + (5 + 13) = 0
-2x2- 5x - 18 = 0
Gebruik discriminant D, hieruit volgen twee antwoorden.
D = b2 - 4ac
D = (- 5)2 + 4 * -2 * -18 = 25 + 144 = 169
x1 = (- - 5 + √(169)) / (2 * -2) = (5 + 13) / -4 = -18/4
x2 = (- - 5 - √(169)) / (2 * -2) = (5 - 13) / -4 = 8/4
Invullen in één van (of beide) grafieken geeft f(-18/4) = 155/4, g(-18/4) = 155/4
Verder geeft f(8/4) = 3, g(8/4) = 3
Ergo, de snijpunten zijn (-18/4, 155/4) en (2, 3)
[/OLIST]