Hoe wordt een gemetselde tuinmuur berekend?
Om een leuke afscheiding in de tuin te hebben, kan men een tuinmuur metselen. Op een stevige fundering kan men de stenen gaan opmetselen, zodat er een duidelijke afbakening ontstaat. Toch kun je niet zomaar tot iedere hoogte en muur maken. Tot hoe hoog kun je een gemetselde tuinmuur maken (uitgaande van verschillende tuinmuur-doorsneden), waarbij het windbestendig is en voldoende constructieve veiligheid heeft?Gemetselde tuinmuur berekenen
- Verschillende doorsnede mogelijkheden bij halfsteense opbouw
- Noodzaak berekenen samengesteld traagheidsmoment
- Belastingen en eisen
- Hoe hoog mag een gemetselde tuinmuur zijn?
- Conclusie meest gunstige tuinmuur
Verschillende doorsnede mogelijkheden bij halfsteense opbouw
Stel je voor er zijn een drietal verschillende muren, waarbij de sterkte moet worden doorgerekend. De eerste vorm is een halfsteense muur dik 105 mm, waarbij om 2,3 m een anderhalfsteense penanten van vierkant 320 mm worden aangebracht. Alles staat op de centrale lijn. Een tweede vorm waarbij de penanten worden toegepast is als één zijde gelijk wordt doorgetrokken met de muur, waardoor een T-vormige doorsnede ontstaat. Een derde vorm is de verspringende wand waarbij per penant een Z vorm ontstaat. Hoe kan de sterkte van het metselwerk worden doorgerekend en hoe hoog mag de wand zijn?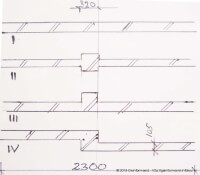
Bron: Http://geinformeerd.infoteur.nlNoodzaak berekenen samengesteld traagheidsmoment
Het traagheidsmoment voor een standaard vierkant wordt bepaald middels Ix = 1/12*b*h^3 met b is breedte en h is hoogte in millimeters. Voor een gewone halfsteenswand zonder penanten zou het per meter 1/12*1000*105^3 = 96*10^6 mm^4 bedragen, oftewel over 2,3 m is dat 222*10^6 mm^4. Indien er penanten worden toegepast dan neemt de sterkte echter aanzienlijk toe. Hoe wordt dit per voorgaande doorsneden berekend?:- halfsteensmuur zonder penanten = Ix = 222*10^6 mm^4 met Wx = 222*10^6/(105/2) = 4,23*10^6 mm^3;
- centrale opstelling muur en penanten = Ix = 1/12*(2300-320)*105^3+1/12*320^4 = 1,065*10^9 mm^4 met Wx = 1,065*10^9/160 = 6,66*10^6 mm^3.
T-vormige opstelling berekend met Steiner
- S = moment oppervlak = 105*2300*105/2+320*215*212,5 = 27,3*10^6 mm^3;
- y = inwendig neutrale lijn ligt op = 27,3*10^6 / (105*2300+320*215) = 88 mm;
- x;doorgaande wand+ St.verplaatsing = 1/12*2300*105^3+2300*105*(88-105/2)^2 = 0,526*10^6 mm^4;
- x;resterende penantdeel + St.verplaatsing = 1/12*320*215^3+320*215*(212,5-88)^2 =1,332*10^6 mm^4;
- Ix;T = 0,526*10^6 + 1,332*10^6 = 1,858*10^9 mm^4;
- Wx;T;max = 1,858*10^9 / 88 = 21,1*10^6 mm^3;
- Wx;T;min = 1,858*10^9/(320-88) = 8,0*10^6 mm^3.
Z-vormige opstelling berekend met Steiner
- y = centrale lijn doorsnede oftewel;
- x;uiterste 2 wanddelen + St.verplaasting = 2*1/12*990*105^2+2*990*105*(160-105/2)^2 = 2,404*10^9 mm^4;
- x;penant = 1/12*320^4 = 0,874*10^9 mm^4;
- x;Z = 2,404*10^9 + 0,874*10^9 = 3,278*10^9 mm^4;
- Wx;Z = 3,278*10^9/160 = 20,49*10^6 mm^3.
Bron: Http://geinformeerd.infoteur.nlBelastingen en eisen
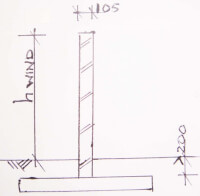
Een metselmuur staat normaal buiten en zal voornamelijk worden belast met wind. Uitgaande van windgebied III bij een veiligheidsklasse 1 kan het met:- qd;wind = 1,2 * (0,8 druk + 0,4 zuiging) * 0,46 kN/m2 worden belast.
De sterkte van de wand is daarbij afhankelijk van de hoogte van het metselwerk. Des te hoger het is des te meer wind vangt het op en treedt er meer momentspanning op. Het optrendende moment M en de normaalspanning N worden als volgt bepaald:
- Md = hoh * qd * l (lengte) * x (arm inclusief inklemming) = hoh * qd * h * (h/2+0,2) = 2,3 * (1,2*1,2*0,46) * h * (h/2+0,2);
- Nd/A = 0,9 * 18,5 (soortelijk gewicht metselsteen) * h.
Hierbij geldt de volgende eis waaraan minimaal moet worden voldaan:
- σ;md = Md/W – Nd/A;
- σ;md / ym (materiaalfactor) < 1,5*0,2/1,8 = 0,166 N/mm^2 = f;md (maximale hechtspanning metstelwerk).
Hoe hoog mag een gemetselde tuinmuur zijn?
Omdat in voorgaande een kwadratische h zit verwerkt kun je het niet zo gemakkelijk handmatig snel benaderen. Via Excel kun je voorgaande verhouding wel snel invullen waarbij:- 0,166 > 2,3*1,2*1,2*0,46*10^6*h*(h/2+0,2)/W-0,9*18,5*h*10^(-3) in verschillende cellen kunt invoeren.
In stappen van 10 centimeter resulteert het in de maximale hoogte van het metselwerk voor de voorgaande doorsneden in:
- halfsteenswand 0,8 m = 1,53*10^6*0,8*(0,8/2+0,2)/4,23*10^6 – 0,9*18,5*0,8*10^(-3) = 0,160 N/mm2;
- centrale opstelling penant 1 m = 1,53*10^6*1,0*(1,0/2+0,2)/ 6,66*10^6 – 0,9*18,5*1,0*10^(-3) = 0,144 N/mm2;
- T;wand;slappe zijde 1,2 m = 1,53*10^6*1,2*(1,2/2+0,2)/8,0*10^6 – 0,9*18,5*1,2*10^(-3) = 0,164 N/mm2;
- T;wand;sterke zijde 2,1 m = 1,53*10^6*2,1*(2,1/2+0,2)/21,1*10^6 – 0,9*18,5*2,1*10^(-3) = 0,155 N/mm2;
- Z;wand 2,1 m = 1,53*10^6*2,1*(2,1/2+0,2)/20,49*10^6 – 0,9*18,5*2,1*10^(-3) = 0,161 N/mm2.