Het deeltje-golf dualisme: grondslag van de kwantummechanica
 In onze wereld van de klassieke mechanica van Newton zijn bewegingen van lichamen voorspelbaar en is energie niet gekwantificeerd. Bij bestudering van elektromagnetische straling introduceerde Max Planck in 1900 de relatie E=hf die hij aanduidde met energie kwantum en in deze relatie ligt de oorsprong van de kwantummechanica, de mechanica van het atoom en de subatomaire wereld. In 1905 bevestigde Einstein dat energie kwanta bestaan en niet alleen een wiskundig begrip zijn. Afhankelijk van het experiment toont licht een golf- of een deeltjeskarakter. Golf en deeltje zijn begrippen uit onze macrowereld en moeten hier niet letterlijk opgevat worden, beter is te spreken van deeltje- en golf-achtige entiteiten. Nog ongewoner is dat er voor de meting geen deeltje is, het ontstaat pas door de meting zelf.
In onze wereld van de klassieke mechanica van Newton zijn bewegingen van lichamen voorspelbaar en is energie niet gekwantificeerd. Bij bestudering van elektromagnetische straling introduceerde Max Planck in 1900 de relatie E=hf die hij aanduidde met energie kwantum en in deze relatie ligt de oorsprong van de kwantummechanica, de mechanica van het atoom en de subatomaire wereld. In 1905 bevestigde Einstein dat energie kwanta bestaan en niet alleen een wiskundig begrip zijn. Afhankelijk van het experiment toont licht een golf- of een deeltjeskarakter. Golf en deeltje zijn begrippen uit onze macrowereld en moeten hier niet letterlijk opgevat worden, beter is te spreken van deeltje- en golf-achtige entiteiten. Nog ongewoner is dat er voor de meting geen deeltje is, het ontstaat pas door de meting zelf.Inhoud
- De geschiedenis van het golf-deeltje dualisme
- Diffractie: het afbuigen van licht- of materiegolven
- De constante van Planck
- Foto-elektrisch effect
- Dubbelspleetexperiment
- Onbepaaldheidsrelatie van Heisenberg
- De Schrödingervergelijking
- Kwantumsprongen
- Verstrengeling
- EPR experiment en de verstrengeling
- Interpretatie van de kwantum theorie
- Samenvatting en conclusies
 Thomas Young experiment in 1802: licht gedraagt zich als een golf / Bron: Publiek domein, Wikimedia Commons (PD)
Thomas Young experiment in 1802: licht gedraagt zich als een golf / Bron: Publiek domein, Wikimedia Commons (PD)De geschiedenis van het golf-deeltje dualisme
- 17de eeuw: Huygens beweert dat licht uit golven bestaat, volgens zijn tijdgenoot Newton echter bestaat licht uit deeltjes. (Achteraf hadden ze allebei gelijk.)
- 1802: Thomas Young voert zijn experiment uit en toont daarmee het golfkarakter van het licht aan.
- 1905: Einstein toont aan met zijn experimenten met het foto-elektrisch effect dat licht ook uit deeltjes (fotonen) kan bestaan.
- 1924: Het golfkarakter van elektronen wordt geponeerd door de natuurkundige De Broglie.
- 1925: Schrödinger stelt zijn golfvergelijking op waarmee het gedrag van een subatomair deeltje - in termen van waarschijnlijkheid - voorspeld wordt.
- 1926: Heisenberg stelt zijn onbepaaldheidsrelatie op.
- 1927: Bevestiging van de golfeigenschappen van deeltjes door vaststelling van verstrooiing en interferentie in het dubbelspleetexperiment. De materiegolven treden op bij alle deeltjes van atomaire afmetingen.
- 1961: Dubbelspleetexperiment met elektronen door Claus Jönsson, waarin hij het bestaan van materiegolven bevestigt.
Links een gat in de plaat die vele malen groter is dan de golflengte van het doorstromende licht- of elektronengolf. Rechts een spleet in de plaat die ongeveer van dezelfde grootte is als de golflengte van de licht- en elektronengolven, hier treedt diffractie op.
 Diffractie van het licht door een enkele spleet / Bron: Dicklyon, Wikimedia Commons (Publiek domein)
Diffractie van het licht door een enkele spleet / Bron: Dicklyon, Wikimedia Commons (Publiek domein) Diffractiepatroon van rood licht op een scherm dat door een enkele klein rond gat is gestraald / Bron: Wisky, Wikimedia Commons (CC BY-SA-3.0)
Diffractiepatroon van rood licht op een scherm dat door een enkele klein rond gat is gestraald / Bron: Wisky, Wikimedia Commons (CC BY-SA-3.0)Diffractie: het afbuigen van licht- of materiegolven
Diffractie (buiging) ontstaat door zijdelingse impulsen in een spleet met een spleetbreedte van dezelfde ordegrootte als de golflengte van de passerende fotonen of elektronen.Door een sleuf in de spletenplaat, die veel groter is dan de golflengte van het invallende licht, gaat de lichtgolf ongestoord heen. Op de achterliggende scherm ontstaat een lichtvlek in dezelfde vorm als het gat in de spletenplaat.
Door een smalle spleet in de plaat, met ongeveer de breedte van de golflengte van het invallende licht, worden de lichtstralen afgebogen door diffractie en waaieren uit volgens de afbeeldingen. Maken we de spleet steeds smaller, dan waaien de lichtstralen verder naar buiten uit.
De constante van Planck
Uit het spectrum van uitgestraalde elektromagnetische golven blijkt dat energie niet continu traploos toe- of af neemt, maar trapsgewijs. De energie van het uitgezonden licht varieert met: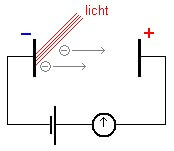 Principe van het foto-elektrisch effect. Zo wordt licht omgezet in elektrische stroom / Bron: DieterM, Wikimedia Commons (CC BY-SA-3.0)
Principe van het foto-elektrisch effect. Zo wordt licht omgezet in elektrische stroom / Bron: DieterM, Wikimedia Commons (CC BY-SA-3.0)Foto-elektrisch effect
Met het foto-elektrisch effect toonde Einstein aan dat licht behalve een golf- ook een deeltjeskarakter heeft, het z.g.n. foton. Een golf kan geen deeltje zijn en een deeltje geen golf en het begrip golf-deeltje-dualisme ontstond. Het foto-elektrische effect is het uitstoten van elektronen uit een metaaloppervlak door de energie van invallend licht. Energie van invallend licht wordt opgenomen door elektronen die daardoor voldoende kinetische energie (trillingsenergie) krijgen om te ontsnappen. Elke foton van een gegeven frequentie (kleur) van een lichtstraal bezit energie E = hf. Des te intenser het invallend licht (meer fotonen per tijdseenheid) des te meer elektronen worden er per tijdseenheid uitgestoten. De kinetische energie van de uitgestoten elektronen blijkt echter onafhankelijk van de intensiteit van de invallende lichtstralen maar alleen afhankelijk van de frequentie (energie) van het licht. Door verhogen van de frequentie f, in plaats van de intensiteit van de invallende stralen, neemt de gemiddelde kinetische energie van de uitgestoten elektronen toe en worden ze met grotere snelheid (Ek is kinetische energie)weg geschoten.Intensiteit van invallend licht wordt verhoogd: meer fotonen vallen op de metalen plaat dus meer elektronen worden uitgezonden, de energie van het uitgestoten foton verandert niet. Als de frequentie (energie) van invallend licht wordt verhoogd, neemt de energie van de uitgestoten elektronen toe:
De kinetische energie van het weggeschoten elektron is:
Dubbelspleetexperiment
In het dubbelspleetexperiment links treedt diffractie op, de kogels worden verdeeld volgens de afbeelding. Het experiment met fotonen en elektronen afbeelding rechts treedt eveneens diffractie op en daarna interferentie tussen spletenplaat en fotografische scherm.Bij twee parallelle verticale spleten ontstaan afwisselend lichte en donkere verticale strepen naast elkaar op het fotoscherm. De verklaring is dat de lichtgolven in de beide spleten diffracteren en daarna onderling met elkaar interfereren. De golven van spleet 1 en 2 versterken elkaar door positieve interferentie op sommige plaatsen, maar op andere plaatsen heffen ze elkaar op, omdat de golven door diffractie verschillende afstanden afleggen vindt er faseverschuiving t.o.v. elkaar plaats.
Het experiment kan met (licht) fotonen en met materiedeeltjes zoals: elektron, neutron en atoom, uitgevoerd worden. Het interferentiepatroon van elektronen toont ook aan dat materiedeeltjes golfeigenschappen hebben, de z.g.n. materiegolven. Een elektron gaat door de ene of de andere spleet maar de bijbehorende "golf" verspreidt zich blijkbaar in de ruimte en gaat door beide spleten en interfereert achter de spleten met zichzelf.
Deeltjes apart door de spleten
Bij een reeks deeltjes die apart achter elkaar door de spleten gaan, bouwt zich geleidelijk het bekende interferentiepatroon op. Verrassend, want elk apart deeltje 'kent' zijn voorganger en opvolger niet, elke doorgang van een deeltje door een spleet is onafhankelijk van de andere deeltjes, elk deeltje interfereert blijkbaar met zichzelf. De plaats die een elektron treft op het fotoscherm wordt bepaald door verdeling van de kansen volgens de kansverdeling.
Door welke spleet gaat een deeltje
In een gedachtenexperiment van de natuurkundige Feynman worden de elektronen direct na de dubbele spleet met licht bestraald. Een foton botst tegen het elektron en dat wordt door een detector geregistreerd. Het foton met de resterende energie wordt uitgezonden in een andere richting dan de invalshoek. Omdat de energie van het foton afneemt, neemt de golflengte toe, des te lager de energie van het foton des te groter de golflengte.
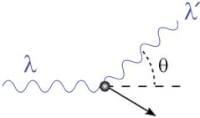 Een foton met golflengte λ komt van links, en botst tegen het elektron. Het elektron krijgt een kinetische energie. Het foton verliest diezelfde energie en zijn golflengte neemt toe tot λ' / Bron: JabberWok, Wikimedia Commons (CC BY-SA-3.0)
Een foton met golflengte λ komt van links, en botst tegen het elektron. Het elektron krijgt een kinetische energie. Het foton verliest diezelfde energie en zijn golflengte neemt toe tot λ' / Bron: JabberWok, Wikimedia Commons (CC BY-SA-3.0)- dλ = verandering van de golflengte van het invallende licht.
- Me = massa van het elektron.
- Q = verstrooiingshoek.
- h = constante van Max Planck.
- C = lichtsnelheid.
- h/MeC = 2,424.10↑-12 staat bekend als de Comptongolflengte, dat is de golflengte van een foton met de massa van een elektron.
Vervolg:
- λ is bekend.
- λ' wordt gemeten.
- Q is bekend of wordt gemeten, hangt af van de opstelling.
- Plaats van het elektron kan berekend worden.
Onbepaaldheidsrelatie van Heisenberg
In tegenstelling tot de klassieke mechanica beïnvloedt de meting de toestand van het te meten object. Wanneer licht op materie valt heeft het een deeltjes(foton) karakter: Het foton ketst af op het object en wordt geregistreerd door detectoren. Zo bepaalt men de positie van het object en het is bekend waar het elektron zich op het moment van meting bevindt en door welke spleet het is gekomen, maar zijn pad na deze plaatsbepaling is onbekend. We kunnen niet voorspellen waar het elektron het fotoscherm raakt. Des te nauwkeuriger we de oorspronkelijke locatie van het object bepalen, dus des te nauwer de spleet, hoe onzekerder de bepaling van zijn toekomstige pad. Deze relatie heeft Heisenberg (1926) verwerkt tot zijn onbepaaldheidsrelatie. De essentie is hier dat om een kwantum te meten we er een kwantum op los moeten laten en die na de botsing detecteren en waaruit men de plaats van het elektron berekent.Volgens de natuurkundige de Broglie is de golflengte van materie en licht:
De Schrödingervergelijking
De golfvergelijking van Schrödinger beschrijft het verloop van een subatomair deeltje in tijd en ruimte in termen van waarschijnlijkheid, met name interessant voor het gedrag van elektronen en subatomaire deeltjes in het atoom. Van een kanonskogel met massa m waar een kracht F op werkt kan men met behulp van de wetten van de klassieke mechanica (Newton) bepalen waar het ding is op ieder tijdstip, men kan plaats, snelheid en impulsmoment voor elk tijdstip berekenen, men weet waar de kogel terechtkomt.De Schrödingergolfvergelijking speelt in de kwantummechanica een rol vergelijkbaar met de rol van Newton's F = m.a in de klassieke mechanica. De naam golffunctie wekt de suggestie dat het deeltje zoals een golf uitgespreid is in de ruimte (op heel veel plekken tegelijk is). Dit is niet zo, een deeltje heeft maar één bepaalde plaats in de ruimte. De golfvergelijking geeft aan wat de kans is dat een deeltje zich op een bepaald tijdstip bevindt.
De Schrödingergolfvergelijking is een lineaire differentiaalvergelijking. De oplossingen zijn golffuncties waarvan het kwadraat van de amplitude de waarschijnlijkheid aangeeft dat het deeltje zich op die plaats bevindt. De wiskundige formulering van de golfvergelijking valt buiten dit artikel, omdat het neemt een onevenredig groot deel van het artikel in beslag neemt.
Kwantumsprongen
Wanneer een elektron in het atoom van de ene baan naar een andere baan overgaat, verplaatst het zich niet als een gewoon object; het verdwijnt van de ene plek en komt op hetzelfde moment op een andere plek weer tevoorschijn. De sprong kost geen tijd, dit heet een kwantumsprong. Als hier sprake is van een afgelegde weg door het elektron dan moet de snelheid oneindig groot geweest zijn. Volgens de relativiteitstheorie van Einstein kan geen snelheid groter zijn als het licht. Er is dus wat anders aan de hand. Wat er precies gebeurt wordt nog steeds niet begrepen. Ook kan men niet precies bepalen waar het elektron op de nieuwe baan te voorschijn komt, of wanneer het de sprong uitvoert. Men gaat bij de berekeningen uit van waarschijnlijkheden volgens de Schrödinger golfvergelijking. In de praktijk is vele malen bewezen dat deze golfvergelijking nauwkeurige resultaten oplevertRurherford en Bohr
Bohr bedacht dat elektronen om de kern heen draaien en dat iedere baan waarin een elektron zit voor een bepaalde energie staat. Wanneer een elektron van een hogere baan naar een baan met mindere energie valt, zal de restenergie gebruikt worden om licht uit te stralen. Vanwege de fotontheorie zal het energieverschil gelijk moeten zijn aan een geheel getal namelijk hf.
Verstrengeling
Subatomaire deeltjes “communiceren” met elkaar, er is wisselwerking over afstand in de ruimte, zonder dat het tijd kost. De kwantumfysica heft de scheiding tussen waarnemer en kwantumobject op, zoals dat het geval is in de klassieke mechanica waar de meting geen gevolgen heeft voor de het gedrag van een macroscopische object. In de kwantumfysica beïnvloedt de waarnemer het waargenomen object, ze vormen samen een nieuw en groter systeem waarmee het kwantumdeeltje niet ongestoord kan worden geobserveerd. Het verstrengelen lijkt op het gedrag van het elektron in het dubbelspleetexperiment, namelijk het "delen van het elektron" om door beide spleten te gaan en achter de plaat gelijk weer naar elkaar toe gaan door middel van interferentie.EPR experiment en de verstrengeling
In een poging de kwantummechanica te verwerpen (door het belachelijk te maken) ontwierpen Einstein, Podolsky en Rosen (EPR) in 1935 een gedachte-experiment waarmee ze aantoonden hoe belachelijk die was. Zij lichtten een van de kenmerken van de kwantumtheorie eruit, namelijk twee deeltjes die op hetzelfde moment zijn gecreëerd, dat wil zeggen dat ze verstrengeld zijn. Vervolgens schiet je ze in tegengestelde richtingen de ruimte in. Verandert men iets aan de toestand van het ene deeltje dan zal ook het andere deeltje tegelijkertijd veranderen, ongeacht de onderlinge afstand. Einstein dacht dat iedereen dat belachelijk zou vinden. Volgens zijn relativiteitstheorie kan niets zich met een grotere snelheid voortbewegen dan met de lichtsnelheid en hier ging het om oneindige snelheid. Het idee dat een elektron contact kon hebben met een ander elektron aan de andere kant van het universum was in strijd met het "gezonde" verstand.John Bell
John Bell ontwierp in 1964 een theorie die de EPR-aanname correct verklaarde. Dat is precies wat er gebeurt; het idee dat een deeltje op één plaats bestaat, is onjuist, deeltjes zijn niet-plaatsgebonden. De deeltjes zijn met elkaar verbonden op een niveau die ons begripsvermogen overstijgt.
Interpretatie van de kwantum theorie
In onze zichtbare wereld geldende de wetten van Newton, in de wereld van ‘de atomen’ gelden de kwantumwetten. De klassieke fysica is deterministisch d.w.z. is de toestand van een lichaam bekend zoals positie en snelheid, kan met nauwkeurig de baan ervan worden bepaald. In de wereld van het atoom gaat dat niet. De kwantumfysica werkt met waarschijnlijkheden. Een en hetzelfde ‘kwantumobject’ kan een deeltje zijn op een bepaalde plaats, maar ook een golf die zich verspreidt in de ruimte. De kwantummechanica schetst een beeld van het heelal als een samenhangend geheel, een groot lichaam waarvan de delen onderling met elkaar verbonden zijn en elkaar beïnvloeden.Deeltje, golf en golfdeeltje
De subatomaire deeltjes - ‘bestanddelen’ van het atoom - zijn geen vormvaste ‘knikkers’. Afhankelijk van hoe we ernaar kijken (meten), zijn ze deeltje- of golfachtig. Een deeltje kan mathematisch worden beschreven als vaste object met een specifieke plaats in de ruimte. Golven zijn niet in een vast punt te lokaliseren maar breiden zich uit zoals rimpels in een vijver.
Golven spreiden zich uit in de ruimte. Niet gemeten elektron gedraagt zich golfachtig. Zodra we meten, stort de golf in tot een deeltje-achtige elektron. Hoe kan een vast deeltje ook een golf zijn? Subatomaire deeltjes gedragen zich als golf of als deeltje. Beter is het de aanduidingen golf-achtig en deeltje-achtig, te gebruiken; het zijn niet echt materiedeeltjes en klassieke golven zoals wij die kennen in de macrowereld.
De Kopenhagen interpretatie
Indien achter de spleten via contact tussen meetinstrument en deeltje wordt vastgesteld welk pad een deeltje neemt (spleet 1 of spleet 2), verdwijnt het interferentiepatroon. In de Kopenhagen interpretatie zegt men dat de golffunctie instort. De Kopenhagen interpretatie zegt dat het deeltje pas ontstaat als de meting wordt verricht, de meting werd niet aan een deeltje verricht, maar veroorzaakte het deeltje. Omdat de meting van het deeltje met een lichtfoton (laser) van dezelfde orde van grootte is als het te meten deeltje is er sprake van verstoring van het deeltje. Men kan de golffunctie zien als een reëel object, óf als een wiskundige truc zonder fysische eigenschappen, waarvan de taak is het berekenen van de waarschijnlijkheid van een gebeurtenis op atomaire schaal. Dit laatste is het standpunt van de meeste wetenschappers.
De Broglie-Bohm interpretatie
De Broglie-Bohm interpretatie van de kwantummechanica is deterministisch, d.w.z. als de uitgangspositie van een deeltje op moment (t1) bekend is, kan zijn positie op tijdstip (t2) berekend worden. De niet deterministische karakter van kwantumverschijnselen worden door De Broglie en Bohm toegeschreven aan de onmogelijkheid de begintoestand van de kwantumobject nauwkeurig genoeg te bepalen.
Oorzaak en gevolg in de klassieke mechanica
In de klassieke mechanica bestaan plaats X en impuls P onafhankelijk van elkaar. Als de toestand van een gesloten systeem op een bepaald tijdstip volledig bekend is, kan zijn vroegere en latere toestand berekend worden. Verleden en toekomst liggen vast. Elke verandering heeft een oorzaak, we spreken van “de wet van oorzaak en gevolg” en van een deterministische wereld.
Oorzaak en gevolg in de kwantummechanica
In de kwantummechanica, staat de golffunctie voor de toestand in een atomair systeem. We kunnen alleen in termen van waarschijnlijkheid zeggen dat een deeltje op een bepaalde plek terechtkomt. In de macroscopische wereld is het wel mogelijk wiskundig te berekenen waar een kanonskogel neerkomt.
Samenvatting en conclusies
De meting aan een subatomair deeltje brengt het kwantumsysteem in contact met de buitenwereld, namelijk met het meetinstrument. Het deeltje en het meetgereedschap vormen samen een nieuw systeem dat te groot is om het gedrag van deeltjes in de kwantumfysica te tonen, de meting verstoort de wereld van het atoom.Een kwantumdeeltje kan verschillende toestanden innemen. Bij het foto-effect gedraagt een foton zich als een deeltje en bij het dubbele spleet experiment blijkt dezelfde foton, wegens het vermogen tot interfereren, golf-achtig.
De natuurwetenschap wordt 'vreemd'
Elementaire deeltjes hebben een golfkarakter en golven een deeltjeskarakter. Dat één subatomair deeltje door twee spleten tegelijk gaat en een deeltjeskarakter krijgt als het achter de spleten contact heeft met een meetinstrument, kunnen we niet begrijpen. Vóór de waarneming bezat de entiteit tegelijkertijd beide mogelijke toestanden, superpositie genoemd en bij meting aan deze entiteit wordt dat één toestand, in geval van de dubbelspleet proef een deeltje- achtige entiteit.
Thomas van Aquino
Atomen en subatomaire deeltjes, waaruit atomen bestaan, worden minder 'materie-achtig'. Het is een deeltje maar het heeft ook een golfkarakter. Thomas van Aquino zegt: “we weten niet wat god is, maar we denken te weten wat hij niet is”, dat begint op de begrip problemen in de kwantummechanica te lijken.
De toekomst ligt niet vast
De kwantummechanica bewijst dat de toekomst niet vastligt, dat de wereld niet, zoals algemeen gedacht in de 19de eeuw, deterministisch is, d.w.z. dat als we de begin toestand van een systeem kennen, de ontwikkeling in het systeem te voorspellen is, m.a.w. de toekomst vastligt als een uurwerk.
Het atoom is voornamelijk lege ruimte
Atomen, de bouwstenen van het stoffelijke heelal, bestaan verreweg het grootste deel uit lege ruimte (circa 99.99% lege ruimte). Als we het waterstofatoom miljarden malen vergroten tot de afmeting van een boerderij, dan heeft de atoomkern de afmeting van een kleine knikker en het elektron is kleiner als een speldenknop, die zich ergens in het rieten dak bevindt. Als we er langs lopen zien we geen atoom, we zien helemaal niets, ondanks de enorme vergroting. Overigens die zogenaamde 'leegte' is niet leeg, maar is waarschijnlijk pure energie.