Wiskunde

Het vermoeden van Goldbach
Het vermoeden van Goldbach is een van de bekendste onopgeloste problemen uit de wiskunde. Het stelt dat "ieder even getal groter dan 2, kan geschreven worden als som van twee priemgetallen". Goldbach…Wat zijn logaritmen?
Dit artikel gaat over verschillende soorten logaritmen; veel gebruikte functies uit de wiskunde. Verder worden ook de rekenregels behandeld die van toepassing zijn bij het rekenen met logaritmen.Hoe bereken je machtsfuncties?
Wat zijn machtfuncties? Machtfuncties zijn functies in de wiskunde die bekend worden geacht voor het centraal eindexamen havo/vwo. Ook buiten de school kunnen machtfuncties gebruikt worden in het dage…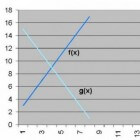
Wiskunde: snijpunten van twee functies bepalen
Hoe bepaal je het snijpunt van twee wiskundige functies? Dit is een belangrijk vraagstuk in de wiskunde. Twee rechte lijnen hebben precies een snijpunt, behalve wanneer de lijnen evenwijdig zijn. Een…Priemgetallen begrijpen
Priemgetallen zijn waarschijnlijk de meest bekende getallen binnen de wiskunde, en dan met name getaltheorie. Maar wat zijn priemgetallen? En wat maakt ze bijzonder? In dit artikel is onder andere uit…Trucjes om snel te kunnen hoofdrekenen
Kun jij 12 × 13 uit je hoofd berekenen binnen 5 seconden? Of 97 × 85? Daar hoef je namelijk geen rekenwonder voor te zijn! Er bestaan vele trucs om erg snel bepaalde berekenen uit het hoofd te doen.…Het bewijzen van de stelling van Pythagoras
In dit artikel wordt uitgelegd hoe de stelling van Pythagoras op twee manieren bewezen kan worden. Het is geschreven voor geïnteresseerden die hun inzicht in deze beroemde stelling willen vergroten.…Exponentiële functies opstellen
Het opstellen van exponentiële functies is een vereiste voor het centraal examen van het VWO, ook wel bekend als het Atheneum. Voor meer informatie over het opstellen van exponentiële functies, het…Vergelijkingen oplossen met algebra
In de moderne wiskunde is oplossen met algebra steeds belangrijker aan het worden. In iedere lesmethode is hier iets over terug te vinden. Ook wordt het oplossing van vergelijkingen bekend geacht bij…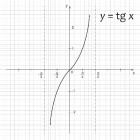
Booleaanse algebra van George Boole
Het Booleaanse algebra wordt nog dagelijks onbewust gebruikt door vele surfers op het web. Door woorden te gebruiken als ‘en’, ‘of’ en ‘niet’ hebben wij al te maken met Booleaanse algebra,…Globale wapeningsberekening
Bij een balk op twee steunpunten veroorzaakt het moment buiging in de balk. Door deze buiging zullen aan de bovenzijde druk- en aan de onderzijde trekspanningen onstaan.Berekenen van betonconstructie
Dit gebeurt aan de hand van afmetingen en belastingen. Op de betonconstructie, of een gedeelte daarvan, kunnen verschillende krachten verwerken. De krachten veroorzaken verschillende soorten spanninge…Rekenmethodes en algoritmes
Er zijn veel verschillende methodes om te leren rekenen. Een methode wordt een algoritme genoemd. Elke wiskundige bewerking van getallen is in feite terug te leiden op een toegepast algoritme, zo ook…Kwadratische vergelijkingen oplossen
Er zijn vier verschillende kwadratische vergelijkingen op te lossen. Het is daarom altijd belangrijk om eerst te kijken welke soort het is voordat je hem probeert op te lossen.
Wiskunde de afgeleide en differentiëren
De afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y). Het geeft de waarde van de richtingcoëfficiënt van de raaklijn in (x,y) aan.…Stelsels van lineaire vergelijkingen oplossen
Een stelsel van lineaire vergelijkingen bestaat uit meerdere vergelijkingen en heeft meerdere onbekenden. We bespreken hier twee methoden om een stelsel van lineaire vergelijkingen met twee onbekenden…
Vergelijkingen oplossen (3): exponentiële vergelijkingen
In dit deel zullen we verschillende soorten exponentiële vergelijkingen bespreken en oplossen. Exponentiële vergelijkingen hebben veel praktische toepassingen buiten de wiskunde. Voorbeelden hiervan…